P5905 [Template] All-Pairs Shortest Paths (Johnson).

Given a directed graph with $n$ nodes and $m$ weighted edges, find the shortest path length between every pair of nodes. The length of a path is defined as the sum of the weights of all edges on the path. Note: 1. Edge weights **may** be negative, and the graph **may** contain multiple edges and self-loops. 2. Some testdata is designed to make running SPFA for $n$ rounds fail.

Line $1$: Two integers $n, m$, representing the number of nodes and the number of directed edges in the given graph. Next $m$ lines: Each line contains three integers $u, v, w$, meaning there is a directed edge of weight $w$ from node $u$ to node $v$.

If the graph contains a negative cycle, output only one line: $-1$. If the graph does not contain a negative cycle: Output $n$ lines. Let $dis_{i,j}$ be the shortest path from $i$ to $j$. On line $i$, output $\sum\limits_{j=1}^n j\times dis_{i,j}$. Note that this value may exceed the range of `int`. If there is no path from $i$ to $j$, then $dis_{i,j}=10^9$; if $i=j$, then $dis_{i,j}=0$.

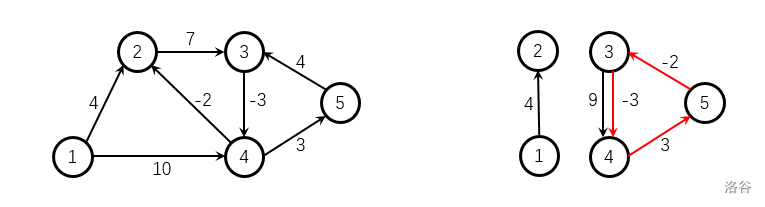
[Sample Explanation] The left figure shows the directed graph given in sample $1$. The answer matrix formed by the shortest paths is: ``` 0 4 11 8 11 1000000000 0 7 4 7 1000000000 -5 0 -3 0 1000000000 -2 5 0 3 1000000000 -1 4 1 0 ``` The right figure shows the directed graph given in sample $2$. The edges marked in red form a negative cycle. Note that the given graph may be disconnected.  [Constraints] For $100\%$ of the data, $1\leq n\leq 3\times 10^3,\ \ 1\leq m\leq 6\times 10^3,\ \ 1\leq u,v\leq n,\ \ -3\times 10^5\leq w\leq 3\times 10^5$. For $20\%$ of the data, $1\leq n\leq 100$, and there is no negative cycle (can be used to verify Floyd correctness). For another $20\%$ of the data, $w\ge 0$ (can be used to verify Dijkstra correctness). upd. Added a set of hack testdata: targeting the SLF optimization of SPFA. Translated by ChatGPT 5