P5948 [POI 2003 R1] Chocolate

There is an $n\times m$ rectangular chocolate bar, and you want to cut it into $n\times m$ small pieces. On the chocolate there are $n-1$ horizontal lines and $m-1$ vertical lines. Each time, you may cut the chocolate along one of these horizontal or vertical lines. No matter how long the cut is, the costs of cutting along the horizontal lines (one time per line) are $y_1,y_2,\dots,y_{n-1}$ in order, and the costs of cutting along the vertical lines are $x_1,x_2,\dots,x_{m-1}$ in order. 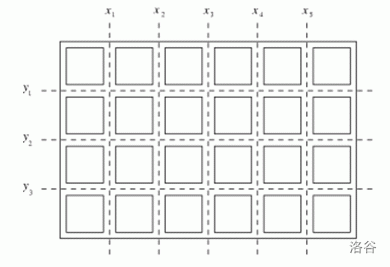For example, for the $6\times 4$ chocolate in the figure below:  If we first cut along three horizontal lines, it takes $3$ cuts and we get $4$ strips of chocolate. Then we cut these $4$ strips along the vertical lines. Each strip needs $5$ cuts, so the total cost is $y_1+y_2+y_3+4\times (x_1+x_2+x_3+x_4+x_5)$. Of course, this simple method may not be optimal. How should you cut the chocolate so that the total cost is minimal?

The first line contains two integers $n$ and $m$. The next $n-1$ lines each contain one integer, representing $x_1,x_2,\dots,x_{n-1}$. The next $m-1$ lines each contain one integer, representing $y_1,y_2,\dots,y_{m-1}$.

Output one integer, the minimum total cost to cut the chocolate.

Constraints: for $100\%$ of the testdata, $1\le n\le 10000$ and $1\le m\le 10000$. Translated by ChatGPT 5