P5971 [CTSC2009] Moving Plates

There are three pegs, named $A$, $B$, and $C$. Initially, $A$ has $N$ plates on it, while $B$ and $C$ are empty. Each move consists of taking the top plate from one peg and placing it onto another peg. Plates are of three types, denoted by $1$, $2$, and $3$. Your goal is to have all type $1$ plates on $A$, all type $2$ plates on $B$, and all type $3$ plates on $C$ in the end. Find the minimum number of moves needed to achieve this goal.

The input file trique.in contains: - The first line: an integer $N$, the total number of plates. - The second line: $N$ numbers, each being $1$, $2$, or $3$. These $N$ numbers describe the types of all plates initially on peg $A$, listed from top to bottom.

The output file trique.out contains a single number: the minimum number of moves.

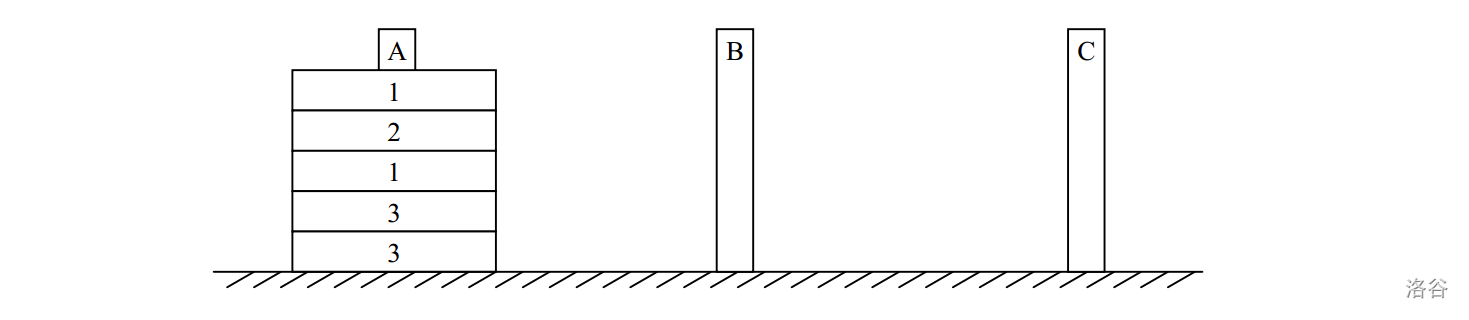
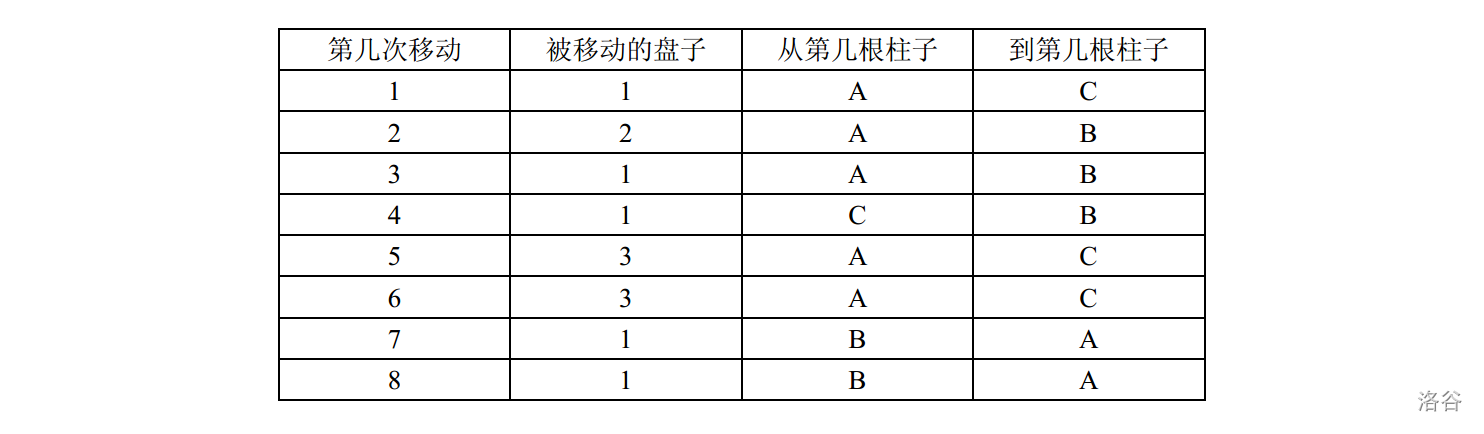
Sample explanation: Initial state as shown below:   Constraints: - For $20$% of the testdata, the number of plate types does not exceed $2$. - For $40$% of the testdata, $N \leq 300$. - For $100$% of the testdata, $N \leq 1000$. Translated by ChatGPT 5