P5983 [PA 2019] Settlements and Fortresses 2

An $n \times m$ grid is given. The rows are numbered from $0$ to $n-1$ from top to bottom, and the columns are numbered from $0$ to $m-1$ from left to right. Initially, every cell is not an obstacle. A path from the start $(0,0)$ to the end $(n-1,m-1)$ is defined to be valid if and only if it passes through exactly $n+m-1$ cells (including the start and the end), and each step moves either one cell to the right or one cell downward. Of course, the path cannot pass through obstacle cells (including the start and the end). You have an $int$ variable $v = 0$. You need to simulate $k$ operations. Each operation gives three non-negative integers $r, c, z$. Let $x = (r \operatorname{xor} v) \bmod n$, $y = (c \operatorname{xor} v) \bmod m$: 1. If $(x,y)$ is an obstacle cell, ignore this operation and output `NIE`. 2. Otherwise, if after turning $(x,y)$ into an obstacle cell there still exists a valid path, then turn $(x,y)$ into an obstacle cell and output `NIE`. 3. Otherwise, if after turning $(x,y)$ into an obstacle cell there is no valid path, then output `TAK`, and update $v$ to $v \operatorname{xor} z$.

The first line contains three positive integers $n, m, k$. The next $k$ lines each contain three non-negative integers $r, c, z$.

For each operation, output one line: `TAK` or `NIE`.

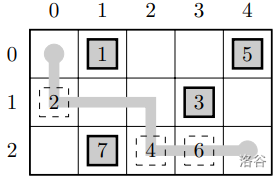
For $100\%$ of the testdata: $2 \le n, m \le 10^5$, $1 \le k \le 10^6$, $0 \le r, c, z < 2^{20}$. ---- ### Explanation:  Translated by ChatGPT 5