P5988 [PA 2019] Wyspa

比特岛位于海上，在比特岛的中心有一个内陆湖。 在比特岛一共有 $n$ 个点，编号为 $1$ 到 $n$，其中 $1$ 到 $a$ 的点按照顺时针或者逆时针表示内陆湖边上的点， $a+1$ 到 $a+b$ 的点按照顺时针或者逆时针表示比特岛海岸线上的点， $a+b+1$ 到 $n$ 的点表示既不在湖边也不在海边的点。 这些点之间连着 $m$ 条单向或双向道路。满足如下限制： - 每条道路不会经过湖、海或者任意其它点。 - 任意两点间只会连着最多一条道路 - 这些道路中不存在“天桥”或者“地下隧道”，任意两条道路只可能在端点处相交，换言之，这是一张平面图。 - 从任意一个湖边的点出发，都能沿着这些道路直接或间接地到达至少一个海边的点。 现在要在 $b$ 个海边点中选择若干个点作为港口，问有多少种选点的方案使得任意一个湖边的点都能到达至少一个港口？

第一行四个正整数 $n,m,a,b$。 接下来 $m$ 行描述 $m$ 条道路，每行要么是 `u -- v` 要么是 `u -> v`($1\le u,v\le n,u\ne v$)： 如果是“`u -- v`，表示这是一条连接 $u$ 和 $v$的双向道路。 如果是 `u -> v`，表示这是一条从 $u$出发到达 $v$的单向道路。

输出一行一个整数，即满足条件的方案数模 $10^9+7$。

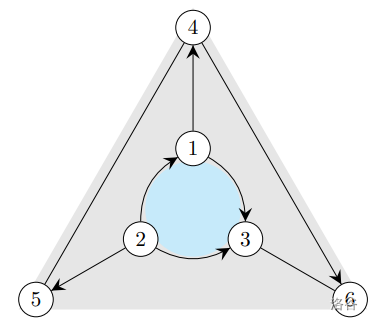
对于 $100\%$ 的数据，$2\le n\le 5\times 10^5$，$1\le m\le 10^6$，$1\le a,b\le n,2\le a+b\le n$。 --- ### 样例解释：  $6$ 号点必选， $4$ 和 $5$ 可选可不选，因此有 $4$种方案。