P5988 [PA 2019] Wyspa

Bit Island is located in the sea, and there is an inland lake in the center of the island. There are $n$ points on Bit Island, numbered from $1$ to $n$. Among them, points $1$ to $a$ (in clockwise or counterclockwise order) represent the points on the shore of the inland lake; points $a+1$ to $a+b$ (in clockwise or counterclockwise order) represent the points on the coastline of Bit Island; points $a+b+1$ to $n$ represent points that are neither on the lake shore nor on the sea shore. There are $m$ directed or undirected roads connecting these points, satisfying the following constraints: - Each road does not pass through the lake, the sea, or any other point. - Between any two points, there is at most one road. - There are no “overpasses” or “underground tunnels” among these roads. Any two roads can intersect only at endpoints; in other words, this is a planar graph. - Starting from any point on the lake shore, one can reach at least one point on the sea shore directly or indirectly along these roads. Now, choose some points among the $b$ sea-shore points as ports. How many ways of choosing ports are there such that every lake-shore point can reach at least one port?

The first line contains four positive integers $n,m,a,b$. The next $m$ lines describe the $m$ roads. Each line is either `u -- v` or `u -> v` ($1\le u,v\le n,u\ne v$): If it is `u -- v`, it means this is an undirected road connecting $u$ and $v$. If it is `u -> v`, it means this is a directed road from $u$ to $v$.

Output one line with one integer: the number of valid ways modulo $10^9+7$.

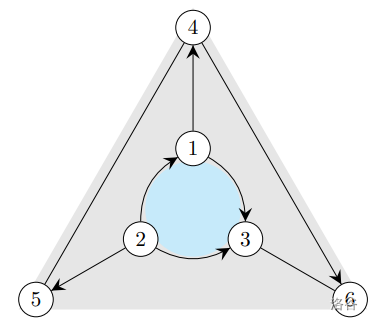
For $100\%$ of the testdata, $2\le n\le 5\times 10^5$, $1\le m\le 10^6$, $1\le a,b\le n$, $2\le a+b\le n$. --- ### Sample Explanation  Point $6$ must be selected, while points $4$ and $5$ may be selected or not, so there are $4$ ways. Translated by ChatGPT 5