P5989 [PA 2019] Wina

A number tower is formed by stacking $\dfrac{n\times(n+1)}{2}$ numbers in $n$ rows. Given $k$, you need to take away exactly $k$ numbers so that the minimum value among the taken numbers is as small as possible. A number can be taken if and only if there is no number at its upper-left and upper-right positions, or those numbers have already been taken.

The first line contains two positive integers $n, k$. The next $n$ lines describe the tower. The $i$-th line contains $i$ positive integers $a[i][1], a[i][2], ..., a[i][i](1\le a[i][j]\le 2019)$, representing the number in the $i$-th row from top to bottom and the $j$-th position from left to right.

Output one integer: the minimum possible value of the minimum among the taken numbers.

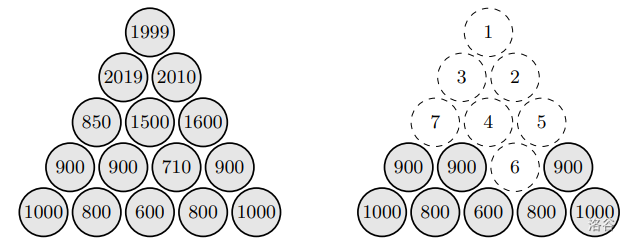
For $100\%$ of the testdata, $1\le n\le 2000$, $1\le k\le \dfrac{n\times(n+1)}{2}$. ### Sample Explanation  Translated by ChatGPT 5