[PA2014] Muzeum

吉丽的漫展有 $n$ 件手办和 $m$ 名警卫。 现在我们对其建立平面直角坐标系，每个手办和警卫都可以看做一个点。警卫们的目光都朝着 $y$ 轴负方向，且都有相同大小的视角。警卫可以看见自己视角内（包括边界上的点）的所有手办，不用考虑视线的遮挡。 你打算抢劫吉丽的漫展，但不想被警卫发现。为了实施这次抢劫计划，你可以事先贿赂某些警卫，让他们闭上眼睛。只要某件手办不在任何睁着眼睛的警卫的视野内，你就可以偷走它。你知道每件手办的价格，以及每位警卫需要接受多少钱的贿赂。你想知道自己的最大收益是多少。

第一行两个整数 $n,m$，分别表示手办的数量和警卫的数量。 第二行两个整数 $w,h$，表示每个警卫的视角的一半的正切值是 $\dfrac{w}{h}$。（见配图） 接下来 $n$ 行，每行三个整数 $x_i,y_i,v_i$，表示手办的坐标为 $(x_i,y_i)$，价格为 $v_i$。 接下来 $m$ 行，格式同上，表示警卫的坐标为 $(x_i,y_i)$，需接受贿赂的金额为 $v_i$。 **保证每个点最多只有一个手办或一个警卫。**

输出仅一行表示最大收益。

5 3
2 3
2 6 2
5 1 3
5 5 8
7 3 4
8 6 1
3 8 3
4 3 5
5 7 6

6

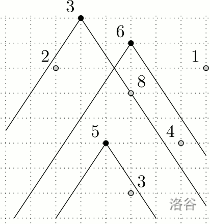
对于 $100\%$ 的数据，$1\le n,m\le 2\times 10^5$，$1\le w,h\le 10^9$，$-10^9\le x_i,y_i\le 10^9$，$1\le v_i\le 10^9$。 ---- ### 样例解释：  贿赂 售价为 $3+6=9$ 元的两个警卫，偷走 价值共$2+8+4+1=15$ 元的 $4$ 个手办，收益 $15-9=6$ 元。