P5996 [PA 2014] Museum

Gili’s convention has $n$ figurines and $m$ guards. Now we build a 2D Cartesian coordinate system for it. Each figurine and each guard can be regarded as a point. All guards look toward the negative direction of the $y$-axis, and they all have the same field of view. A guard can see all figurines inside its field of view (including points on the boundary). You do not need to consider any blocking of the line of sight. You plan to rob Gili’s convention, but you do not want to be discovered by the guards. To carry out this plan, you may bribe some guards in advance to make them close their eyes. As long as a figurine is not in the field of view of any guard whose eyes are open, you can steal it. You know the price of each figurine and the amount of money required to bribe each guard. You want to know your maximum profit. **It is guaranteed that each point contains at most one figurine or one guard.**

The first line contains two integers $n, m$, representing the number of figurines and the number of guards. The second line contains two integers $w, h$, meaning that the tangent of half of each guard’s viewing angle is $\dfrac{w}{h}$. (See the figure.) The next $n$ lines each contain three integers $x_i, y_i, v_i$, meaning that the figurine is at $(x_i, y_i)$ and its price is $v_i$. The next $m$ lines have the same format, meaning that the guard is at $(x_i, y_i)$ and the bribe amount required is $v_i$.

Output one line containing the maximum profit.

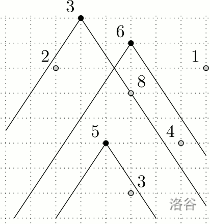
For $100\%$ of the testdata, $1\le n,m\le 2\times 10^5$, $1\le w,h\le 10^9$, $-10^9\le x_i,y_i\le 10^9$, $1\le v_i\le 10^9$. ---- ### Sample Explanation  Bribe two guards whose total bribe is $3+6=9$, and steal $4$ figurines whose total value is $2+8+4+1=15$, so the profit is $15-9=6$. Translated by ChatGPT 5