P6027 Axial Symmetry

Little W learned axial symmetry transformations.

Little W thinks axial symmetry transformations are really fun, so he randomly picked $n$ points $A_1,A_2,\cdots,A_n$ on the plane, and then performed a series of axial symmetry transformations to obtain $n$ points $B_1,B_2,\cdots,B_n$, where $A_1$ becomes $B_1$, and so on. However, he suddenly forgot how he transformed them, so he asks you to help him find a valid sequence of transformations with as few steps as possible.

The first line contains an integer $n$, the number of points. The next $n$ lines, line $i+1$ contains two real numbers $x,y$, representing the $x$- and $y$-coordinates of $A_i$. The next $n$ lines, line $i+n+1$ contains two real numbers $x,y$, representing the $x$- and $y$-coordinates of $B_i$.

The first line contains an integer $k$, the minimum number of steps. The next $k$ lines, line $i+1$ contains three real numbers $A,B,C$, indicating that the axis of the $i$-th axial symmetry transformation is the line $Ax+By+C=0$.

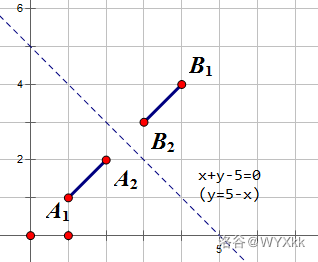
## Sample Explanation  ## Hint For the line $Ax+By+C=0$, if $B$ is non-zero, then it is the graph of the linear function $y=-\dfrac ABx-\dfrac CB$; otherwise, it represents a line perpendicular to the $x$-axis, namely $x=-\dfrac CA$. This problem uses an $\text{SPJ}$. **For some reason, this problem does not provide** the $\text{SPJ}$ **to contestants.** For each test case, if your $k$ is correct, you will get $30\%$ of the score. Next, we will apply your $k$ axial symmetry transformations to $A_1,A_2,\cdots,A_n$ respectively, and let the resulting point of $A_i$ be $C_i$. If for all $i$, the absolute differences between the $x,y$ coordinates of $B_i$ and $C_i$ are both no more than $10^{-2}$, then you will get $100\%$ of the score. If you only want to output $k$, please also output some arbitrary values afterwards to avoid $\text{UKE}$. ## Constraints | Test Point ID | $n=$ | Number of folds used when constructing the testdata | | ---------- | ---- | -------------------- | | 1,2 | $1$ | $\le1$ | | 3,4 | $2$ | $\le10$ | | 5,6 | $5$ | $\le10^3$ | | 7,8,9,10 | $10$ | $\le10^5$ | For all data, $1\le n\le10$, $|x|,|y|\le 10^5$. All data points have been verified by the $\text{SPJ}$ and are correct. Please ensure that all $A,B,C$ in your output satisfy $|A|,|B|,|C|\le 10^5$. Translated by ChatGPT 5