P6037 Ryoku’s Exploration.

Ryoku is very curious about the world she lives in. Before she “dies”, she hopes to explore as much of the world as possible. One day, Ryoku got a map of this world and was very happy. However, Ryoku does not know where she is, and she also does not know when she will die. She wants to know how to explore as much of this world as possible.

Ryoku’s world can be modeled as a weighted, undirected, connected graph $G$ with $n$ vertices and $n$ edges. Each edge has a beauty value and a length. Ryoku explores the world using the following strategy: at each vertex, among the edges whose **endpoint she has not visited yet**, she chooses the one with the **highest beauty value** to walk along. If there is no edge to take, she returns along the edge she used to reach this vertex, similar to a graph **depth-first traversal**. The length of an exploration plan is the sum of the lengths of all edges that the plan walks through (the distance walked when returning does not need to be counted). She wants to know, for every starting vertex $s=1,2,\cdots,n$, what total length she needs to walk.

The input contains $n+1$ lines. The first line contains an integer $n$. The next $n$ lines each contain four integers $u,v,w,p$, describing an undirected edge connecting $u$ and $v$, with length $w$ and beauty value $p$.

Output $n$ lines, each containing one integer. The $i$-th line is the answer when $s=i$.

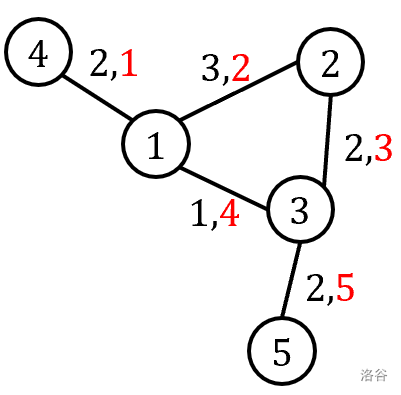
**[Sample 1 Explanation]** The following is the graph in Sample Input/Output 1 (the red numbers on edges are $p$, and the black numbers are $w$).  If the starting point is $1$, the order is $1\to3\to5\to2\to4$, and the sum of lengths is $7$. If the starting point is $2$, the order is $2\to3\to5\to1\to4$, and the sum of lengths is $7$. If the starting point is $3$, the order is $3\to5\to1\to2\to4$, and the sum of lengths is $8$. If the starting point is $4$, the order is $4\to1\to3\to5\to2$, and the sum of lengths is $7$. If the starting point is $5$, the order is $5\to3\to1\to2\to4$, and the sum of lengths is $8$. --- **[Constraints]** For $40\%$ of the testdata, $n\le 10^3$. For $100\%$ of the testdata, $3 \le n \le 10^6$, $1 \le u,v,p \le n$, $0\le w\le 10^9$. It is guaranteed that all $p$ are distinct. Translated by ChatGPT 5