P6038 「ACOI2020」惊吓路径

 3 年 E 班的同学们赢得了去南方的冲绳小岛的机会，在渚打败了鹰冈之后，他们受杀老师的邀请参加“试胆大会”。 试胆大会在一个黑漆漆的洞窟里面进行。赤羽 業（Akabane Karma）现在和奧田 愛美站在洞窟的门口。突然，業想到了一个事情。。。

杀老师告诉过他们，洞窟可以近似地看成 $n$ 个点的外向树，因为地形原因，所以一个点到另一个点的边是有方向的，且边的方向都是同向的。这棵树的树根为入度为 $0$ 的点。每个点都有一个惊吓值，给出每个点的惊吓值 $a_i$。 杀老师告诉他们，这个洞穴有很多惊吓路径。如果两个节点 $u,v$ 构成的路径是一条惊吓路径的话，满足以下条件： - $v$ 一定在 $u$ 的子树中。 - $u, v$ 这条路径上的所有的点的惊吓值的或值 $\geq k$。 走过一条惊吓路径就会收到杀老师的惊喜大礼。杀老师已经提前准备好了惊喜大礼，但是業当然已经知道杀老师有一些下流的意图，更别说惊喜大礼的数量可能不够！杀老师已经承诺有多少条惊吓路径就有多少个惊喜大礼。業已经通过一些神奇的途径知道了杀老师准备的惊喜大礼的个数，现在他想知道有多少条惊吓路径，也就是杀老师最少需要准备惊喜大礼的个数。如果不够，他就会揭穿杀老师的意图。现在業当然想赚，好好捉弄一下杀老师。所以他~~作弊~~提前得到了杀老师的地图，想问这个图里面有多少条惊吓路径？

第一行两个整数 $n,k$。 第二行 $n$ 个整数，表示每个点的惊吓值。 接下来 $n-1$ 行，每行有两个整数 $u,v$ 表示节点 $u,v$ 之间有一条有向边，节点 $u$ 可以到达节点 $v$，**节点 $v$ 不可以到达节点 $u$**。

一行一个整数，表示这个洞穴的惊吓路径条数。

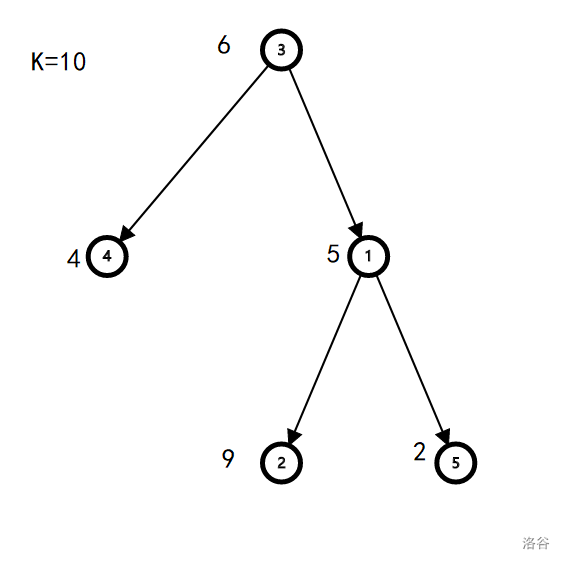
#### 样例解释 #1  只有两条路径满足条件： 1. $3\to 1\to 2$，这条路径的所有点的惊吓值的或值是 $6\operatorname{or}5\operatorname{or}9=15$。 2. $1 \to 2$，这条路径的所有点的惊吓值的或值是 $5\operatorname{or}9=13$。 ------------ #### 数据范围 **本题采用捆绑测试**。 - Subtask 1（10 points）：$n \leq 5 \times 10^3$，$k \leq 10^5$。 - Subtask 2（30 points）：对于任意一条边，$v=u+1$，$n \leq 10^6$，$k,a_i \leq 10^9$。 - Subtask 3（20 points）：$n \leq 10^5$，$k,a_i \leq 10^9$。 - Subtask 4（40 points）：$n \leq 5 \times 10^5$，$k,a_i \leq 10^9$。 对于 $100\%$ 的数据，$1 \leq n \leq 10^6$，$1 \leq k,a_i \leq 10^9$。 ------------ #### 提示 **第四个子任务中的测试点空间 256MB，其余子任务中的测试点空间 128MB。**