P6038 "ACOI2020" Scare Paths.

 The students of Class E, Year 3 won a chance to go to the southern Okinawa island. After defeating Takaoka at Nagisa, they were invited by Koro-sensei to join a “courage test”. The courage test takes place in a pitch-dark cave. Akabane Karma is now standing at the entrance of the cave with Okuda Manami. Suddenly, Karma thought of something...

Koro-sensei told them that the cave can be approximately seen as an out-tree with $n$ nodes. Due to the terrain, the edge from one node to another has a direction, and the directions of all edges are consistent. The root of this tree is the node with in-degree $0$. Each node has a scare value; the scare value of node $i$ is $a_i$. Koro-sensei told them that there are many scare paths in this cave. If the path formed by two nodes $u, v$ is a scare path, then it satisfies: - $v$ must be in the subtree of $u$. - The bitwise OR of the scare values of all nodes on the path from $u$ to $v$ is $\geq k$. Walking through a scare path will earn a “surprise gift” from Koro-sensei. Koro-sensei has prepared the gifts in advance, but Karma already knows Koro-sensei has some improper intentions, not to mention the number of gifts might not be enough. Koro-sensei promised that there would be as many surprise gifts as there are scare paths. Karma has learned, through some mysterious means, how many surprise gifts Koro-sensei prepared. Now he wants to know how many scare paths there are, i.e., the minimum number of gifts Koro-sensei must prepare. If it is not enough, he will expose Koro-sensei’s intentions. Of course, Karma wants to take advantage of this and mess with Koro-sensei. So he ~~cheated~~ got Koro-sensei’s map in advance, and wants to ask: how many scare paths are there in this graph?

The first line contains two integers $n, k$. The second line contains $n$ integers, representing the scare value of each node. The next $n - 1$ lines each contain two integers $u, v$, indicating that there is a directed edge between nodes $u$ and $v$, and node $u$ can reach node $v$. **Node $v$ cannot reach node $u$.**

Output one integer in one line, representing the number of scare paths in this cave.

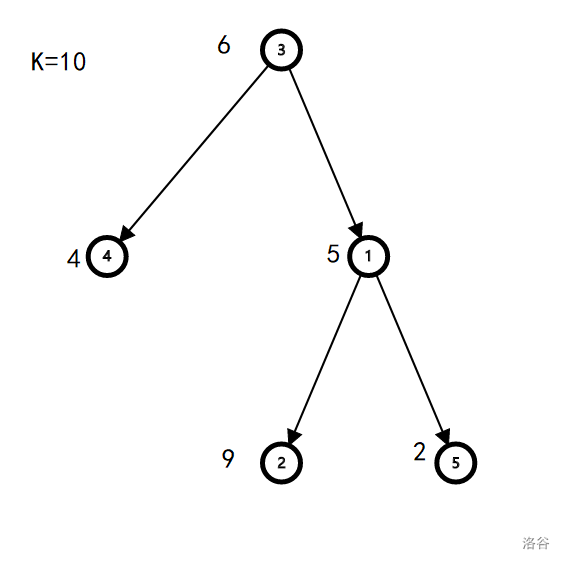
#### Sample Explanation #1  Only two paths satisfy the conditions: 1. $3 \to 1 \to 2$. The bitwise OR of the scare values of all nodes on this path is $6\operatorname{or}5\operatorname{or}9=15$. 2. $1 \to 2$. The bitwise OR of the scare values of all nodes on this path is $5\operatorname{or}9=13$. ------------ #### Constraints **This problem uses bundled testdata.** - Subtask 1 (10 points): $n \leq 5 \times 10^3$, $k \leq 10^5$. - Subtask 2 (30 points): For any edge, $v = u + 1$, $n \leq 10^6$, $k, a_i \leq 10^9$. - Subtask 3 (20 points): $n \leq 10^5$, $k, a_i \leq 10^9$. - Subtask 4 (40 points): $n \leq 5 \times 10^5$, $k, a_i \leq 10^9$. For $100\%$ of the testdata: $1 \leq n \leq 10^6$, $1 \leq k, a_i \leq 10^9$. ------------ #### Note **In the fourth subtask, the memory limit is 256MB; in the other subtasks, the memory limit is 128MB.** Translated by ChatGPT 5