P6047 Silk Cutting.

Pharloom is a mysterious kingdom, where [Silksong](https://www.bilibili.com/video/av43623335) is the strongest power. A multi-string harp is a powerful weapon in Pharloom, just like polynomials are powerful weapons in OI. Because you hate polynomials, you decide to destroy the multi-string harp.

The following part is only to help you understand the idea, and does not explain everything in detail. A more rigorous and clear statement is given in the formal statement. A multi-string harp consists of two pillars and $m$ strings connecting the two pillars. On each pillar, there are $n$ evenly placed fixed points. The $i$-th string connects the $u_i$-th fixed point on the upper pillar and the $v_i$-th fixed point on the lower pillar.  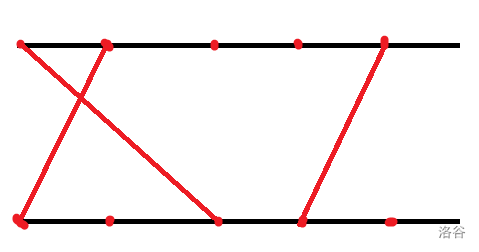> The picture above shows a multi-string harp. To destroy the multi-string harp, you can perform several cutting operations. In one cutting operation, you may choose a fixed point $u$ on the upper pillar and a fixed point $v$ on the lower pillar. All strings that are crossed **from left to right** by the line segment from $u$ to $v$ will be destroyed. At the same time, you need to pay a cost of $a_u \times b_v$. Formal statement: There are $m$ strings. A string can be abstracted as an ordered pair $(u,v)$. You may perform any number of cutting operations. In one cutting operation, you choose two indices $i$ and $j$ such that $i,j \in [1,n]$, and then all strings $(u,v)$ satisfying $u>i,v

The first line contains two integers $n,m$. The second line contains $n$ integers $a_1,a_2,\dots,a_n$. The third line contains $n$ integers $b_1,b_2,\dots,b_n$. The next $m$ lines each contain two integers $u,v$, indicating a string $(u,v)$. The meaning of the input is as described in the statement.

Output one integer in one line, the answer.

#### Sample Explanation For the first sample, use two cuts, namely $(1,3)$ and $(3,5)$, with total cost $3 \times 1 + 1 \times 3 = 6$. For the second sample, note that cutting $(5,1)$ cannot make the string $(3,3)$ disappear. --- #### Constraints **This problem uses bundled testdata.** For all test points, it is guaranteed that $1 \leq n, m \leq 3\times 10^5$, $2 \leq u \leq n$, $1 \leq v \leq n-1$, and $1 \leq a_i,b_i \leq 10^6$. $\text{Subtask 1 (21 pts)}$ $n,m \leq 6$. $\text{Subtask 2 (3 pts)}$ $m=1$. $\text{Subtask 3 (1 pts)}$ $a_1=b_n = 1$. $\text{Subtask 4 (25 pts)}$ $n,m \leq 100$. $\text{Subtask 5 (29 pts)}$ $n,m \leq 10^3$. $\text{Subtask 6 (21 pts)}$ No additional constraints. --- #### Hint If you look carefully at the constraints, you will find that this multi-string harp can always be destroyed. Translated by ChatGPT 5