P6049 Fanji

Compute the number of labeled rooted trees that satisfy the following conditions: - The tree has $n$ nodes in total. - Each node has an integer weight in the range $[1,m]$. - The weight of each node is **not greater than** the weight of its parent. The answer may be very large. Output the value modulo $998244353$. Two trees $T_1$ and $T_2$ are different if and only if they have different numbers of nodes, or different roots, or there exists a label $i$ such that the parent label of node $i$ is different in $T_1$ and $T_2$, or the weight of node $i$ is different.

One line with two positive integers $n,m$, as described above.

One line with one integer, the required answer.

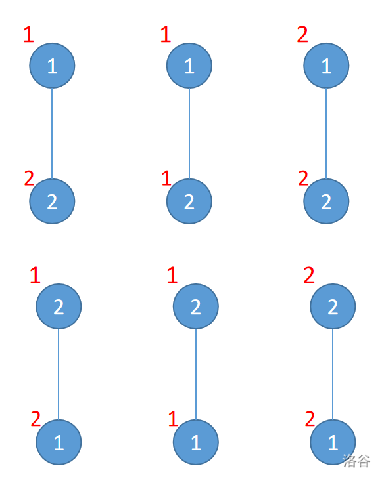
#### Sample Explanation For the first sample,  The six trees are shown in the figure above. The number inside each circle is the node label, and the number outside each circle is the node weight. --- #### Constraints **This problem uses bundled testdata.** For all test cases, it is guaranteed that $1 \leq n \leq 400$ and $1 \leq m < 998244353$. $\text{Subtask 1 (7 pts)}$ $n = 3, m = 3$. $\text{Subtask 2 (11 pts)}$ $m = 1$. $\text{Subtask 3 (19 pts)}$ $n, m \leq 6$. $\text{Subtask 4 (17 pts)}$ $n \leq 7$. $\text{Subtask 5 (11 pts)}$ $n, m \leq 50$. $\text{Subtask 6 (35 pts)}$ No special constraints. Translated by ChatGPT 5