P6050 [RC-02] 游戏

Shik 大佬发明了一种游戏。这种游戏在 $N \times N$ （$N$ 为偶数）的网格上进行，如图所示（左上角为 $(1,1)$，右下角为 $(N,N)$）：  这种游戏的规则如下： - 初始局面为：在最左边一列和最右边一列的网格上分别放置着红方和蓝方的棋子，在最上面一行左半部分和最下面一行左半部分也放置着红方的棋子，在最上面一行右半部分和最下面一行右半部分也放置着蓝方的棋子； - 红方先走，蓝方后走； - 有一方只剩下 $N\div 2$ 颗棋子时，游戏结束，另一方获胜； - 有一方无棋可走时，游戏结束，另一方获胜； - 每次走棋可以让一颗棋子往上下左右方向移动 $1$ 格，但目标格上不能有棋子； - 同时满足以下条件时可以吃掉对方棋子：在一行（或一列上），有且仅有 $N-1$ 颗棋子（当 $N>4$ 时为 $N-2$ 颗也可），其中有 $N-2$ 颗己方棋子（当 $N>4$ 时为 $N-3$ 颗也可），另外 $1$ （当 $N>4$ 时为 $2$ 颗也可）颗棋子为敌方的，我方的棋子全部相邻，敌方棋子全部相邻，并且我方有一颗棋子与敌方相邻，**而且此局面为我方主动走成**，则我方可以把这一列上敌方的棋子全部吃掉。 现在，请你模拟走棋的过程。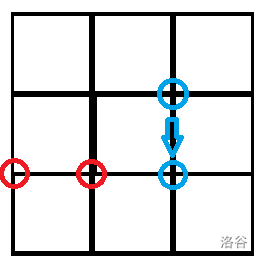  以上为一个不可以吃子的局面。（红吃蓝） 但假如蓝棋本来就在 $(3,3)$，红棋从 $(2,2)$ 走到 $(2,3)$，就可以吃子。 **若不能理解，强烈建议手推一遍样例。**

输入文件的第一行有两个整数 $N$ 和 $K$，表示棋盘的大小和走棋的总步数。 接下来 $K$ 行，每行四个整数 $a,b,c,d$，表示某一方的原本在 $(a,b)$ 的棋子走到了 $(c,d)$。从第二行开始算起，第偶数行表示蓝方，第奇数行表示红方。

分三种情况输出答案： - 数据不合法：输出 $0$。 - 这一局还没有结束：第一行输出 $1$，接下来 $N$ 行，每行 $N$ 个字符，表示目前的局面状态。用```h```表示红方棋子，```l```表示蓝方棋子，```.```表示此网格为空。若此局面某一方可以吃子，输出吃子后的状态。 - 这一局已经结束：第一行输出 $2$，第二行输出```red```或```blue```，表示哪一方获胜。第三行至第 $N+2$ 行，输出获胜时的局面。用```h```表示红方棋子，```l```表示蓝方棋子，```.```表示此网格为空。若此局面某一方可以吃子，输出吃子后的状态。**你的程序应该忽略使你判断出胜负那一行之后的所有输入。**

样例 4 说明：第 21 歩时，红方已胜，因此第 22 歩的非法移动应该忽略。 对于 $30\%$ 的数据，不存在吃子的情况； 对于 $60\%$ 的数据，$N=4$； 对于 $80\%$ 的数据，$4\le N\le 6$； 对于 $100\%$ 的数据，$4\le N\le 10$，$1 \le K \le 10^3$。