P6058 [Cheer Up Wuhan] Temperature Survey.

After the outbreak spread, medical staff from the CDC (Center for Disease Control) made home visits to people coming from Wuhan and measured their temperatures. The staff start from the CDC, visit all households in a fixed order, and then summarize the data. The household list records addresses like `Street A, Community B, Building C, Unit D`, and it is sorted in lexicographical order, so households in the same region are always adjacent in the list. After the staff finish visiting all households in one region (for example, Community B1), they need to submit the data to the management office at the upper level (for example, Street A), and then continue visiting households in another region (for example, Community B2). That is, the moving route looks like a **tree**: the root represents the CDC, the leaves represent households, and the middle nodes represent management regions level by level. The children of a node represent the next-level regions (or households), and they are ordered. All nodes on the path from the root to a household form exactly the address of that household.  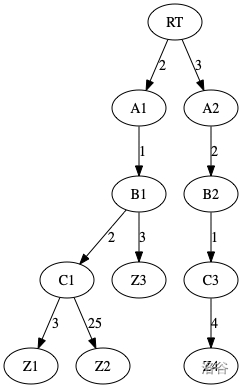As shown in the figure, the addresses of the 4 households are (in order): - A1-B1-C1-Z1 - A1-B1-C1-Z2 - A1-B1-Z3 - A2-B2-C3-Z4 The arrows only represent the belonging relationship, and all edges can be traveled in both directions. In essence, the tree given in the problem is a **lexicographical trie** / **Trie tree** built from the addresses.

Given a tree whose root node is numbered $1$. A medical worker starts from the root, moves along the edges, collects information from every leaf, and finally returns to the root. The visiting order is fixed: whenever he reaches a node $u$, he first goes to the child with the smallest index, visits all households in that child subtree and comes back to $u$, then goes to the child with the second smallest index, and so on, until all households in the subtree of $u$ have been visited and he returns to the parent. It can be seen that the order of visiting leaves is exactly the order in the household address list. Moving along an edge takes time. To save time, we may split the household list into $k$ continuous segments, and let $k$ medical workers start from the root at the same time. Each worker visits the households in one segment and then returns. Please compute the minimum time needed to finish collecting temperatures for all households.

The first line contains two integers $n, k$, representing the number of nodes in the tree and the number of medical workers. The next $n-1$ lines each contain three integers $u, v, w$, representing an edge between $u$ and $v$, with travel time cost $w$.

Output one integer in one line, representing the minimum time needed to finish the temperature survey for all households.

For $30\%$ of the testdata, $1 \le n \le 20$. For another $10\%$ of the testdata, $k = 1$. For another $20\%$ of the testdata, $k = 2$. For $100\%$ of the testdata, $1 \le n \le 2*10^5$, $1 \le k \le m$, $1 \le u, v \le n$, $0 \le w \le 10^9$, where $m$ is the number of leaves. ### Sample Explanation See the figure in the Background. The first person’s route is RT->Z1->Z2->RT, costing 66. The second person’s route is RT->Z3->Z4->RT, costing 32. The plan where one person visits Z2 and the other visits Z1, Z3, Z4 is invalid. Translated by ChatGPT 5