P6076 [JSOI2015] Coloring Problem

Mengmeng has a chessboard. It is an $n \times m$ rectangle, divided into $n$ rows and $m$ columns, for a total of $n \times m$ small cells. Now Mengmeng and Nannan have $C$ different colors of paint. They want to color the chessboard using these paints and satisfy the following rules: 1. Each cell on the board can either be colored (painted in one of the $C$ colors) or left uncolored. 2. Each row of the board has at least one colored cell. 3. Each column of the board has at least one colored cell. 4. Each color appears on the board at least once. 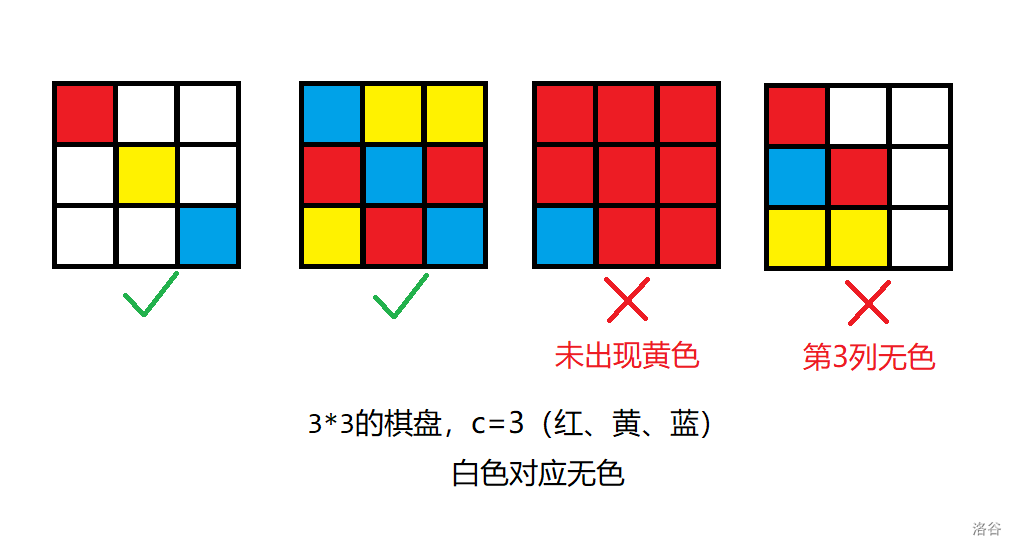Below are some examples of coloring a $3 \times 3$ board with $C=3$ colors (red, yellow, blue) (the figure has been updated):  Compute the total number of different valid coloring schemes that satisfy the requirements. If there exists at least one position whose color is different, then the two coloring schemes are considered different.

The input contains only one line with $3$ integers $n, m, c$.

Output one integer, the total number of different coloring schemes. Since the total number may be very large, output the value modulo $1,000,000,007$.

For $100\%$ of the testdata, $1 \le n, m, c \le 400$. Translated by ChatGPT 5