P6090 [CEOI 2019] Cube Word Filling.

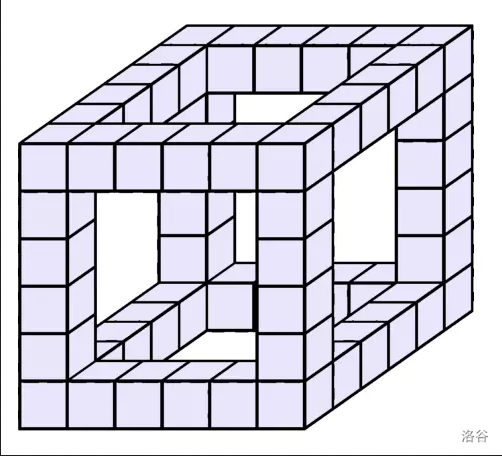
Cube word filling is a special kind of word-filling game. Before filling, you need to choose the edge length $a$ of a cube, and then you can build a cube consisting of $a^3$ unit cubes. This large cube has $12$ edges. Then, you remove all unit cubes that do not touch any edge of the large cube. The figure below shows the final cube when $a = 6$.  Finally, you need to fill a letter into each remaining unit cube. After filling, the word along each edge of the large cube should be meaningful. Each edge can be read in both directions; it is enough if it forms a meaningful word in at least one direction. The figure below shows a cube when $a = 6$. Some unit cubes have already been filled with letters. You can already read three words along three edges of the large cube: **SUBMIT**, **ACCEPT**, and **TURING**.  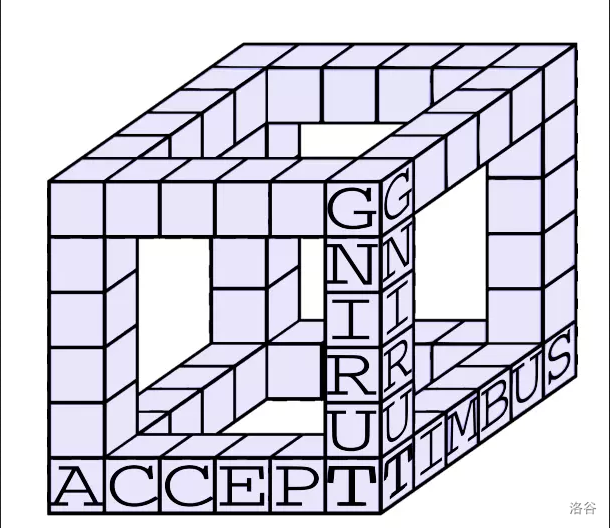Given a list of meaningful words, each word may appear on any edge of a valid cube. Find how many different cubes can be constructed, modulo $998244353$. Even if one cube can be transformed into another by rotations and reflections, they are still considered **different**.

The first line contains an integer $n$, the number of words. The next $n$ lines each contain one word, indicating a word that may appear on an edge of the large cube. The word length is at least $3$ and at most $10$. It is guaranteed that all words are distinct.

Output one integer, the number of different cubes that can be constructed modulo $998244353$.

#### Sample Explanation #1 In the first sample, the only possibility is that the word on every edge of the cube is **radar**. #### Sample Explanation #2 In the second sample, there are two cubes, and one can be obtained from the other by rotation. The words on all edges are **robot**. The difference between the two cubes is whether the letter in the bottom-left corner is **r** or **t**. #### Sample Explanation #3 The third sample is similar to the second one. Note that the reading direction does not affect the answer. #### Sample Explanation #4 In the fourth sample, if you fill **bob** on every edge of the cube, there is one cube. There are also $2^{12} = 4096$ cubes where every edge is filled with **baobab** (for each of the $12$ edges, there are two possible reading directions). #### Constraints For all testdata, $1 \le n \le 10^5$. The detailed subtask constraints and scores are shown in the table below: | Subtask ID | Constraint | Score | | :----------: | :----------: | :----------: | | 1 | Words contain only lowercase `a` to `f` | $21$ | | 2 | Words contain only lowercase `a` to `p` | $29$ | | 3 | Words contain lowercase `a` to `p` and uppercase `A` to `P` | $34$ | | 4 | Words contain lowercase `a` to `z`, uppercase `A` to `Z`, and digits `0` to `9` | $16$ | Translated by ChatGPT 5