P6137 [IOI 2012] Ideal City

Like many scientists and artists of his age, Little L is very interested in city planning and urban design. He is devoted to building an ideal city. The ideal city consists of $N$ blocks, and these blocks are placed on an infinite square grid. The cell in row $x$ and column $y$ is identified by the ordered pair $(x,y)$. The cell $(0,0)$ is located at the upper-left corner of the grid. Given a cell $(x,y)$, the adjacent cells (if they exist) are: $(x-1,y)$, $(x+1,y)$, $(x,y-1)$, $(x,y+1)$. Each block covers exactly one cell on the grid. A block can be placed on cell $(x,y)$ if and only if $1 \le x,y \le 2^{31}-2$. We will use the coordinates of a cell to also denote the block on that cell. If two blocks are placed in adjacent cells, they are considered adjacent blocks. All blocks in the ideal city are connected, and there are no “holes” inside. In other words, all cells must satisfy the following two conditions: - For any two empty cells, there exists at least one sequence of adjacent empty cells connecting them. - For any two non-empty cells, there exists at least one sequence of adjacent non-empty cells connecting them. The block placements in the following $4$ figures do not satisfy the conditions of an ideal city. The first two figures do not satisfy the first condition. The $3$rd figure does not satisfy the second condition, and the $4$th figure satisfies neither condition.  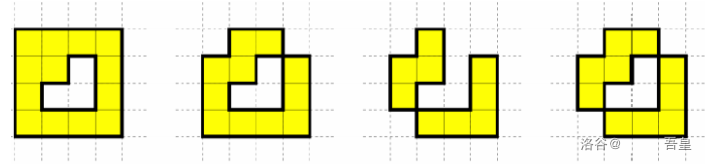When traversing the ideal city, one **step** means **moving from one block to an adjacent block**. During a step, you cannot move into an empty cell. Suppose $v_0,v_1,\cdots,v_{N-1}$ are the coordinates of the $N$ blocks. For any two different blocks $v_i$ and $v_j$, their distance $d(v_i,v_j)$ is the minimum number of steps needed to move from $v_i$ to $v_j$. The figure below shows an ideal city consisting of $11$ blocks. 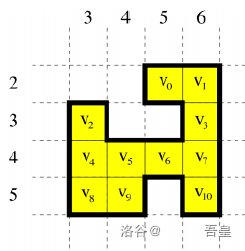The block coordinates are:  $$v_0=(2,5) \quad v_1=(2,6) \quad v_2=(3,3)$$ $$v_3=(3,6) \quad v_4=(4,3) \quad v_5=(4,4)$$ $$v_6=(4,5) \quad v_7=(4,6) \quad v_8=(5,3)$$ $$v_9=(5,4) \quad v_{10}=(5,6)$$ Here, $d(v_1,v_3)=1$, $d(v_1,v_8)=6$, $d(v_6,v_{10})=2$, and $d(v_9,v_{10})=4$. Given an ideal city, compute $$S=\sum_{i=0}^{N-2}\sum_{j=i+1}^{N-1}d(v_i,v_j)$$

The first line contains a positive integer $N$, the number of blocks in the ideal city. Lines $2$ to $N+1$ each contain two non-negative integers. Line $i+2$ gives the coordinates of the $i$-th block $v_i = (x_i, y_i)$.

Output a single line containing a positive integer, the value of $S$. Since $S$ may be very large, you only need to output $S$ modulo $10^9$.

For $100\%$ of the testdata, $1 \le N \le 10^5$, and $1 \le x_i,y_i \le 2^{31}-2$. Translated by ChatGPT 5