P6158 Blockade

Shocking news! zbw has actually escaped from the prison in City B! As the police chief of City B, you must catch zbw before he escapes from your jurisdiction.

City B can be seen as an $n \times n$ grid. The prison is at $(1,1)$, and the only exit out of City B is at $(n,n)$. Between every two adjacent points (where $|\Delta x| + |\Delta y| = 1$) there is an **undirected** road (there are no diagonal roads). You need to deploy guards on some roads so that no matter how zbw moves, he will have to pass through at least one of these guarded roads. The cost to deploy guards on the road from $(i,j)$ to $(i,j+1)$ is $r_{i,j}$. The cost to deploy guards on the road from $(i,j)$ to $(i+1,j)$ is $d_{i,j}$. Also, deploying guards affects people’s lives. The impact on people’s lives caused by deploying guards on the road from $(i,j)$ to $(i,j+1)$ is $x_{i,j}$, and the impact caused by deploying guards on the road from $(i,j)$ to $(i+1,j)$ is $y_{i,j}$. Let the total cost be $w$, and the total impact be $e$. As an excellent police chief, you need to minimize $w \times e$.

The first line contains an integer $n$. Then there are $n \times (n-1)$ lines. In the $i$-th line, there are two integers $r_{i/n+1,(i-1)\bmod n+1}$ and $x_{i/n+1,(i-1)\bmod n+1}$. Then there are $n \times (n-1)$ lines. In the $i$-th line, there are two integers $d_{i/n+1,(i-1)\bmod n+1}$ and $y_{i/n+1,(i-1)\bmod n+1}$. That is, the information of vertical edges is given first from top to bottom and from left to right, and then the information of horizontal edges is given from top to bottom and from left to right. If you do not understand, please refer to the sample explanation.

Output one integer on a single line, which is the minimum value of $w \times e$.

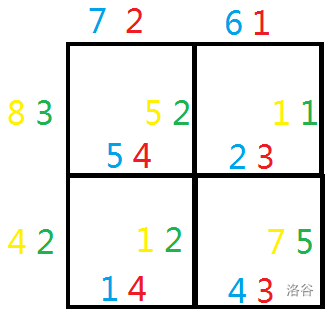
 As shown in the figure, the top-left corner is $(1,1)$ and the bottom-right corner is $(n,n)$. The blue numbers represent $r$, the red numbers represent $x$, the yellow numbers represent $d$, and the green numbers represent $y$. The optimal plan is to guard three edges: $(2,2)-(2,3)$, $(3,1)-(3,2)$, $(3,2)-(3,3)$. The edge weights of the three edges are $2,3$ --- $1,1$ --- $4,3$. The answer is $(1+2+4)\times (1+3+3)=49$. You can see that there is no better solution. **This problem uses bundled testdata.** | Subtasks | $n$ | Special property | Score | | :----------: | :----------: | :----------: | :----------: | | Subtask 1 | $n=2$ | None | $5$ | | Subtask 2 | $n\leq400$ | Random testdata | $15$ | | Subtask 3 | $n\leq10$ | None | $15$ | | Subtask 4 | $n\leq50$ | None | $30$ | | Subtask 5 | $n\leq400$ | None | $35$ | Constraints: for all testdata, $1 \leq n \leq 400$, $0 \leq r_{i,j}, d_{i,j}, x_{i,j}, y_{i,j} \leq 10^3$. The testdata was strengthened on 2020/3/4, removing some solutions with incorrect time complexity. Translated by ChatGPT 5