P6159 [Cnoi2020] Light Diagram

> Greatness is hidden in simplicity. Cirno casually divided a circle with total internal reflection into $12$ equal parts, and the division points are denoted as $A_0$, $A_1$, $A_2$, $\cdots$ , $A_{11}$. Then, she casually emitted a beam of light from one point toward another point. By repeating, reflecting, and iterating, she obtained a beautiful light diagram. All of this happened casually. She casually noticed this scene, and casually wrote down this casual conclusion, and at some moment casually recalled it. Every day in Gensokyo is so carefree. What a nice day.

Rumia has a unit circle, divided into $n$ equal parts, and the division points are denoted as $A_0$, $A_1$, $A_2$, $\cdots$ , $A_{n-1}$. Now she emits a beam of light from $A_0$ toward $A_p$. After $k - 1$ reflections, it arrives at $A_t$. Rumia wants to know the value of $t$. Since Cirno does not want to help her, Rumia turns to you for help.

One line with three integers, $n, p, k$.

One line with one integer $t$.

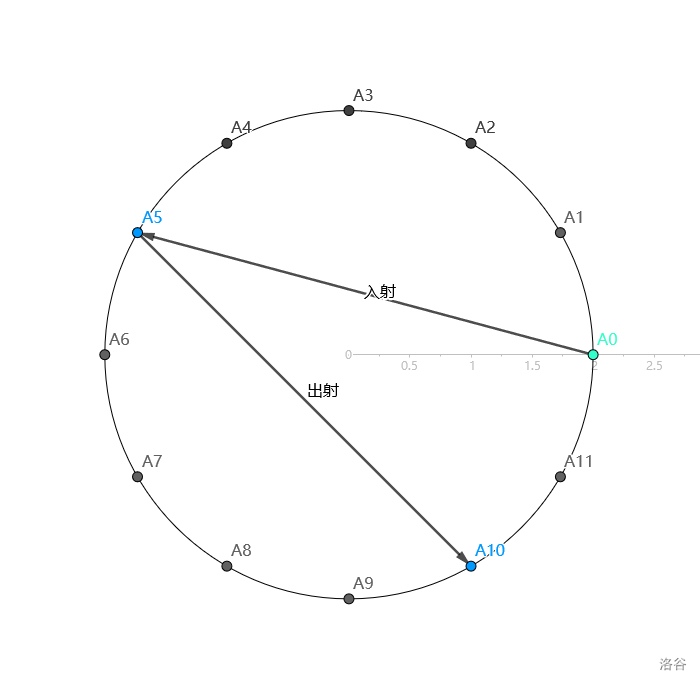
### Explanation of Sample 1  ### Physical knowledge used later - **Reflection law on a continuous curve**: The incident ray and the reflected ray make equal angles with the tangent line of the curve at the point of incidence. ### Constraints **This problem uses bundled testdata.** - Subtask 1 ($80\%$): $n, k \le 10^6$. - Subtask 2 ($20\%$): $n, k \le 10^9$. For $100\%$ of the testdata: $0 < p < n \le 10^9$, $0 < k \le 10^9$. ### Postscript - The light diagram obtained by Cirno is the legendary **twelve-pointed star diagram**. Translated by ChatGPT 5