P6165 [IOI 2012] rings

In Leonardo’s manuscript "Codex Atlanticus", an early and complex parachute was described. Leonardo’s parachute is a pyramid-shaped wooden frame covered with sewn cloth. **Linked rings** A free-fall skydiver, Adrain Nicholas (Ai Zhun Ni Gu La Si), tested Leonardo’s design five hundred years later. In this test, a modern lightweight frame was used to attach Leonardo’s parachute to a human body. We want to use linked rings, which provide hooks for the sewn cloth. Rings can be linked together easily, and each ring can be opened or closed. Linked rings can form a special shape called a "chain". A "chain" is a sequence of linked rings, where each ring can be linked to (at most two) neighbors. However, this sequence must have a beginning and an end (these two rings can each be linked to only one other ring), as shown in the figure below.  Other linking shapes are also possible, because one ring can be linked to 3 or more rings. We say a ring is "critical" if, after we open it and remove this ring, the remaining rings form a collection of pairwise disjoint chains (or no rings remain). 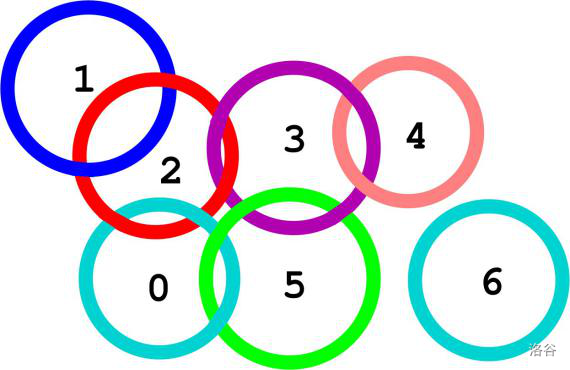**Example** Consider the $7$ rings in the figure below, numbered from $0$ to $6$. In this example, there are two "critical" rings. One critical ring is ring $2$. After removing this ring, the remaining rings form three chains: $[1]$, $[0,5,3,4]$, and $[6]$. Another critical ring is ring $3$. After removing this ring, the remaining rings form three chains: $[1,2,0,5]$, $[4]$, and $[6]$. If we try to remove any other ring, we cannot obtain a collection of pairwise disjoint chains. For example, after removing ring $5$, although we can obtain a chain like $[6]$, rings $0,1,2,3$ and $4$ do not form a chain.  **Task** Given a configuration of linked rings, your program must compute the number of critical rings in it.

- The first line contains $2$ integers $N, L$. $N$ means there are $N$ pairwise disjoint rings, numbered from $0$ to $N-1$, as the initial ring configuration. $L$ is the number of operations. - Lines $2$ to $L+1$ each contain $1$ or $2$ integers, describing an operation as follows: 1. `A B` means linking ring $A$ and ring $B$ together. It is guaranteed that $A$ and $B$ are different. 2. `-1` output one line: the number of critical rings in the current linked-ring configuration.

For each operation of type $2$, output one line: the number of critical rings in the current linked-ring configuration at that time.

For $100\%$ of the testdata, $1 \le N, L \le 10^6$. Translated by ChatGPT 5