P6167 [IOI 2016] shortcut

Pavel has a very simple toy railway. It has a main line with $n$ stations, numbered consecutively from $0$ to $n-1$. Station $0$ and station $n-1$ are at the two ends of the main line. The distance between station $i$ and station $i+1$ is $l_i$ centimeters ($0 \le i < n-1$). Besides the main line, the railway may have some branch lines. Each branch line consists of a new piece of track between one station on the main line and a new station outside the main line (these new stations are not numbered). Each station on the main line can have at most one branch line. The length of the branch starting from station $i$ on the main line is $d_i$ centimeters. We use $d_i=0$ to indicate that station $i$ has no branch line.  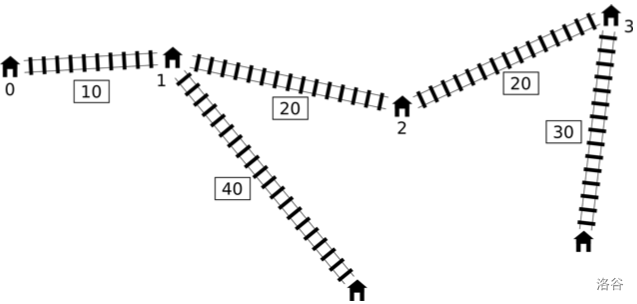Pavel is now planning a shortcut: a fast track between two different stations on the main line (they may be adjacent). No matter which two stations it connects, the length of this fast track will be exactly $c$ centimeters. Every segment of the railway, including the new fast track, can be traveled in both directions. The distance between any two stations is the length of the shortest path between them along the railway. The largest distance among all pairs of stations is called the diameter of the whole railway network. In other words, there exists a minimum value $t$ such that the distance between any two stations does not exceed $t$. Pavel wants to build one fast track so that, after adding it, the diameter of the new railway network is as small as possible. ### Sample 1 ``` 4 10 10 20 20 0 40 0 30 ``` The optimal solution is to build a fast track between station $1$ and station $3$, as shown in the figure below.  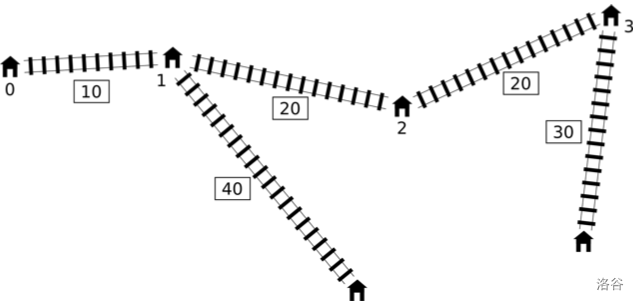The diameter of the new railway network is $80$ centimeters, so you should output $80$. ### Sample 2 ``` 9 30 10 10 10 10 10 10 10 10 20 0 30 0 0 40 0 40 0 ``` The optimal solution is to connect station $2$ and station $7$. The diameter of this solution is $110$. ### Sample 3 ``` 4 1 2 2 2 1 10 10 1 ``` The optimal solution is to connect station $1$ and station $2$, which shortens the diameter to $21$. ### Sample 4 ``` 3 3 1 1 1 1 1 ``` Building a fast track of length $3$ between any two stations will not improve the diameter of the railway network, so the diameter remains the initial value $4$.

- Line 1: Two integers $n$ and $c$. - Line 2: Integers $l_0,l_1,\cdots,l_{n-2}$. - Line 3: Integers $d_0,d_1,\cdots,d_{n-1}$.

Output one line: the minimum possible value of the diameter of the railway network after adding the new fast track.

For $100\%$ of the testdata, $2 \le n \le 10^6$, $1 \le l_i \le 10^9$, $0 \le d_i \le 10^9$, $1 \le c \le 10^9$. Translated by ChatGPT 5