P6204 [USACO07CHN] Treasure G

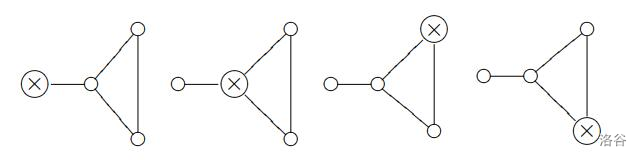
卡门和他的朋友们最近挖到了一箱财宝，他们打算将这箱财宝埋在公路网的某个节点上。 整个公路网有 $N$ 个节点，这些节点之间由 $N$ 条公路连接。公路都是双向通行的，任何一个节点至少与一条公路相连，且没有节点与超过 $4$ 条公路连接。卡门决定不将财宝埋在有 $4$ 条公路连接的节点上，因为那里交通繁忙，容易被暴露。 卡门将公路网的地图画了出来，并在计划埋藏财宝的地方画了个叉。为了研究最佳埋藏方案，他把所有情况都画了出来，比如下面是一个 $N=4$ 时的所有埋藏情况：  他仔细研究后，发现后两种方案是本质相同的。两种地图是本质相同的，当且仅当： - 宝藏埋藏地点相对应； - 如果两个节点间有路，则对应节点间也有路； - 如果两个节点间没有路，则对应节点间也没有路。 现在你需要求出究竟有多少种本质不同的埋藏方案。

第一行一个整数 $N$（$4 \leq N \leq 10^5$）。 接下来 $N$ 行，每行两个整数 $u,v$（$1 \leq u,v \leq N$），描述一条道路。 保证两个节点间最多有一条道路直接相连，且不存在从节点 $u$ 到节点 $u$ 的道路。

输出本质不同的埋藏方案数。