P6204 [USACO07CHN] Treasure G

Carmen and his friends recently dug up a box of treasure. They plan to bury it at some node in a road network. The entire road network has $N$ nodes, and these nodes are connected by $N$ roads. All roads are bidirectional. Every node is connected to at least one road, and no node is connected to more than $4$ roads. Carmen decides not to bury the treasure at a node that has $4$ roads connected to it, because the traffic there is heavy and it is easy to be exposed. Carmen drew a map of the road network and marked an $X$ at the planned burial location. To study the best burial plan, he drew all possible cases. 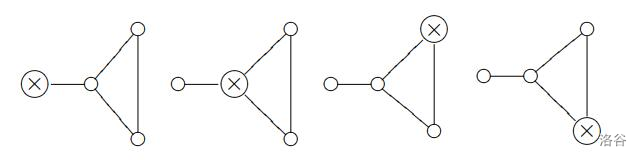For example, the following shows all burial cases when $N=4$:  After careful study, he found that the last two plans are essentially the same. Two maps are essentially the same if and only if: - The treasure burial locations correspond to each other. - If there is a road between two nodes, then there is also a road between the corresponding nodes. - If there is no road between two nodes, then there is also no road between the corresponding nodes. Now you need to find how many essentially different burial plans there are.

The first line contains an integer $N$ ($4 \leq N \leq 10^5$). The next $N$ lines each contain two integers $u, v$ ($1 \leq u, v \leq N$), describing a road. It is guaranteed that there is at most one road directly connecting any two nodes, and there is no road from node $u$ to node $u$.

Output the number of essentially different burial plans.

Translated by ChatGPT 5