P6213 "SWTR-4" Collecting Coins

Little A likes Collecting Coins. He also has a good friend named little c. While traveling outside, little c got trapped in a maze. After hearing the news, little A immediately put down the “tree-of-trees-of-trees” he was playing and set off to rescue her.

After some investigation, little A found that the maze where little c is trapped consists of $n$ rooms, connected by $n-1$ doors, **forming a tree**. Little c is trapped in room $d$. Little A also found that each door has a number $v$ written on it. Passing through that door gives $v$ coins, but the coins on each door can only be obtained once. Since the bad guys who trapped little c already knew little A would come to rescue her, they placed traps in every room, so that room $i$ can be entered at most $k_i$ times; otherwise, little A would also be trapped in the maze. Luckily, when asking little A for help, little c had already told him about this trap. When entering the maze, little A may choose any starting room $r$ (entering the maze counts as entering room $r$ once). **Little A can leave the maze if and only if he is in room $r$.** If little A enters room $d$, we consider that he has successfully rescued little c. After rescuing little c, little A may continue moving in the maze with her. Although little A is not a very greedy person, he still wants to know: under the condition that he **successfully rescues little c** and leaves the maze, what is the maximum number of coins he can obtain.

The first line contains two integers $n,d$, representing the number of rooms and the room number where little c is trapped. The next $n-1$ lines each contain three integers $x_i,y_i,v_i$, representing the two room numbers connected by the $i$-th door, and the number written on that door. The next line contains $n$ integers $k_1,k_2,\cdots,k_n$, representing the maximum number of times each room can be entered.

Output one integer in a single line, representing the maximum number of coins little A can obtain.

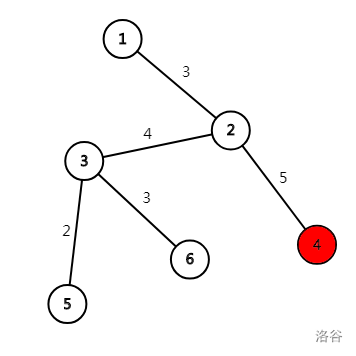
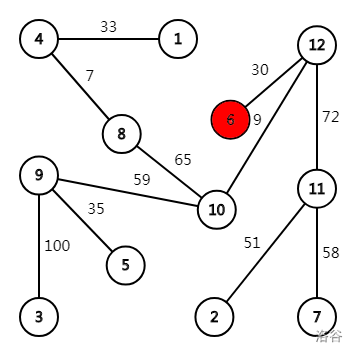
[Sample $1$ Explanation]  One optimal route is: $2\to 4\to 2$, and it can obtain $5$ coins in total. [Sample $2$ Explanation] As in the figure above, little A can only “airdrop” to room $4$, and then leave the maze, obtaining $0$ coins in total. [Sample $4$ Explanation]  One optimal route is: $3\to 9\to 10\to 8\to 10\to 12\to 6\to 12\to 10\to 9\to 3$, and it can obtain $100+59+65+9+30=263$ coins in total. [Constraints and Notes] **This problem uses bundled testdata.** Subtask ID | $n\leq$ | Special Property | Score | :-: | :-: | :-: | :-: | $1$ | $12$ | $k_i=1$ | $3$ | $2$ | $12$ | $k_i\leq 3$ | $12$ | $3$ | $10^3$ | The maze is a chain | $9$ | $4$ | $10^3$ | None | $16$ | $5$ | $10^5$ | The maze is a chain | $9$ | $6$ | $10^5$ | The maze is a “chrysanthemum graph” (juhua tu) | $16$ | $7$ | $10^5$ | None | $35$ | For $100\%$ of the data, $1\leq d,k_i\leq n\leq 10^5$, $1\leq v_i\leq 10^4$. [Source] [Sweet Round 04](https://www.luogu.com.cn/contest/26414)$\ \ $E idea & std: [Alex_Wei](https://www.luogu.com.cn/user/123294), validator: [chenxia25](https://www.luogu.com.cn/user/138400) Translated by ChatGPT 5