P6219 [COCI 2019/2020 #6] Construction

This problem is translated from [LOJ3268](https://loj.ac/problem/3268)。

**Translated from [COCI 2019/2020 Contest #6](https://hsin.hr/coci/archive/2019_2020/) T3.** ***[Konstrukcija](https://hsin.hr/coci/archive/2019_2020/contest6_tasks.pdf)*** Let $G$ be a directed acyclic graph. If distinct vertices $c_1,c_2,c_3,\ldots c_n$ in $G$ satisfy that there is a path from $c_1$ to $c_2$, a path from $c_2$ to $c_3$, ..., and a path from $c_{n-1}$ to $c_n$, then the array $C = (c_1,c_2,c_3,\ldots c_n)$ is called an ordered array that starts at $c_1$ and ends at $c_n$. Note that for any two adjacent elements $c_i,c_{i+1}$ in $C$, there does not have to be a direct edge between them; having a path is enough. We also define the length of an ordered array $C = (c_1,c_2,c_3,\ldots c_n)$ as $\mathrm{len}(C) = n$. Therefore, the length of an ordered array is exactly the number of vertices it contains. Note that an ordered array of length $1$ that starts and ends at the same vertex can exist. Moreover, we define the sign of an ordered array $C = (c_1,c_2,c_3,\ldots c_n)$ as $\mathrm{sgn}(C) = (-1)^{\mathrm{len}(C)+1}$. For vertices $x,y$ in $G$, let $S_{x,y}$ denote the set of all ordered arrays that start at $x$ and end at $y$. Finally, we define the contradiction value between vertices $x,y$ as $\mathrm{tns}(x,y) = \sum\limits_{C \in S_{x,y}} \mathrm{sgn}(C)$. That is, the contradiction value between $x$ and $y$ equals the sum of the signs of all ordered arrays that start at $x$ and end at $y$. Given an integer $K$, you need to construct a directed acyclic graph with at most $1000$ vertices and $1000$ edges such that $\mathrm{tns}(1,N) = K$, where $N$ is the number of vertices. Vertices are numbered by positive integers $1 \ldots N$.

The first line contains one integer $K$。

The first line contains two integers $N,M$, the number of vertices and edges in the directed acyclic graph you construct. In the next $M$ lines, the $i$-th line contains two distinct integers $X_i,Y_i$, meaning the $i$-th edge is directed from $X_i$ to $Y_i$. Each edge should appear at most once. Also, your construction must satisfy that for any two vertices, the absolute value of their contradiction value is at most $2^{80}$. If there are multiple solutions, output any one of them.

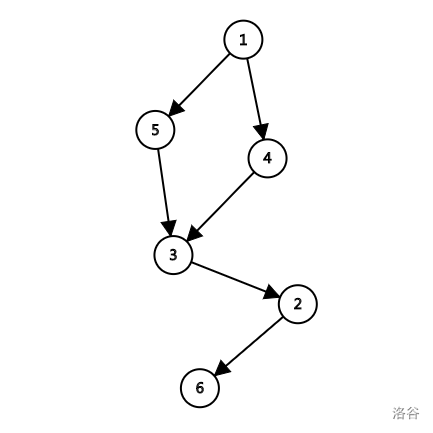
### Explanation for Sample 1 The constructed graph has $6$ vertices. The ordered arrays that start at $1$ and end at $6$ are: - $(1, 6)$； - $(1, 4, 6)$； - $(1, 5, 6)$； - $(1, 3, 6)$； - $(1, 2, 6)$； - $(1, 4, 3, 6)$； - $(1, 4, 2, 6)$； - $(1, 5, 3, 6)$； - $(1, 5, 2, 6)$； - $(1, 3, 2, 6)$； - $(1, 4, 3, 2, 6)$； - $(1, 5, 3, 2, 6)$。 Their lengths are $1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4$, respectively, so their signs are $-1, 1, 1, 1, 1,-1,-1,-1,-1,-1, 1, 1$, respectively. Therefore, the contradiction value between $1$ and $6$ is $-1 + 1 + 1 + 1 + 1 - 1 - 1 - 1 - 1 - 1 + 1 + 1 = 0$。  ----- ### Constraints For $100\%$ of the testdata, $|K| \le 10^{18}$. The limits for each subtask are shown in the table below: |Subtask|Points|Limits| |:-:|:-:|:-:| |$0$|$0$|Sample only| |$1$|$13$|$1 \le K < 500$| |$2$|$13$|$-300 < K \le 1$| |$3$|$18$|$\lvert K\rvert < 10000$| |$4$|$56$|-| Translated by ChatGPT 5