P6232 [eJOI 2019] Hanging Rack

A hanging rack consists of $n$ layers of connecting rods. Layer $i$ ($i\in [0,n-1]$) contains $2^i$ connecting rods. The midpoint of the rod in layer $0$ is fixed to the wall. In every other layer, the midpoint of the $j$-th rod ($j\in[1,2^i]$) is fixed to the $\left\lceil{\dfrac{j}{2}}\right\rceil$-th rod in the previous layer. If $j$ is odd, it is fixed to the left endpoint of that rod; if $j$ is even, it is fixed to the right endpoint. On the bottom layer, each rod has a hook at both its left and right endpoints for hanging clothes. Each hook can hold at most one piece of clothing. 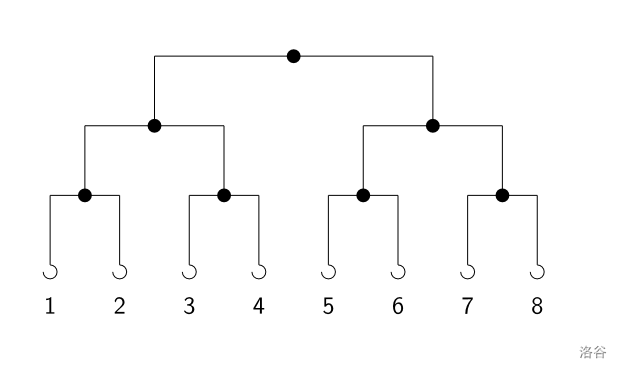For example, when $n=3$, the rack looks like this:  Mojca wants to hang all her clothes on this rack. Each piece of clothing weighs exactly one unit. To avoid breaking the rack’s fragile structure, she must hang the clothes one by one following a specific rule (i.e., in some order): - After hanging one piece of clothing, for every connecting rod, let the total weight below its left endpoint be $w_l$ and below its right endpoint be $w_r$. It must always hold that $w_l-w_r \in {0,1}$. **Note that it must not be** $-1$. The rods and hooks are very light, so their weight can be ignored. Mojca has heard that you are very capable, so she asks for your help. Given two integers $n,k$, determine on which hook the $k$-th piece of clothing should be hung.

The input contains one line with two positive integers $n,k$.

Output one line with a single integer: the index of the hook on which the $k$-th piece of clothing should be hung, taken modulo $(10^9+7)$. **The hook indices are not the same as the connecting rod indices.**

#### Sample Input/Output Explanation **Sample 1 Explanation** - The order of using the hooks should be: $1,5,3,7,2,6,4,8$. Therefore, the second piece of clothing should be hung on hook $5$. **Sample 2 Explanation** - Here, the hooks are used in the order: $1, 17,9, 25,5, 21,13,29,3,19,\text{etc.}$ --- #### Constraints **This problem uses bundled subtasks, with a total of 3 subtasks**. - Subtask 1 (20 points): $n \leq 10$. - Subtask 2 (20 points): $n \leq 20$. - Subtask 3 (60 points): no special restrictions. For all testdata, it is guaranteed that $1 \leq n \leq 10^6$ and $1 \leq k \leq \min(2^n, 10^{18})$. --- #### Notes The original problem is from: [eJOI2019](https://www.ejoi2019.si) Problem B. [Hanging Rack](https://www.ejoi2019.si/static/media/uploads/tasks/rack-isc(1).pdf) Translation provided by: @[```_Wallace_```](https://www.luogu.com.cn/user/61430) (They felt that the [LOJ translation](https://loj.ac/problem/3196) was simplified too much and could cause ambiguity, so they translated it again.) Translated by ChatGPT 5