P6235 [eJOI 2019] Rectangle Coloring
Background
**Warning: Abusing the judging system for this problem will result in your account being banned.**
Description
Srečko wants to color every cell in a rectangular grid with $m$ rows (indexed from $0$ to $m-1$) and $n$ columns (indexed from $0$ to $n-1$). At the beginning, the whole rectangle is white. In each step, he chooses one diagonal and colors all cells on that diagonal. Coloring a diagonal costs a certain amount (ignore its length), so some diagonals may cost more to color than others.
You need to write a program that reads the coloring cost of each diagonal and outputs the minimum total cost to color all cells.
**Note that recoloring the same cell multiple times is allowed.**
------------------------------------
An $m \times n$ rectangular grid has a total of $2n+2m-2$ diagonals.
Example: when $m=4,n=3$, there are $12$ diagonals in total:
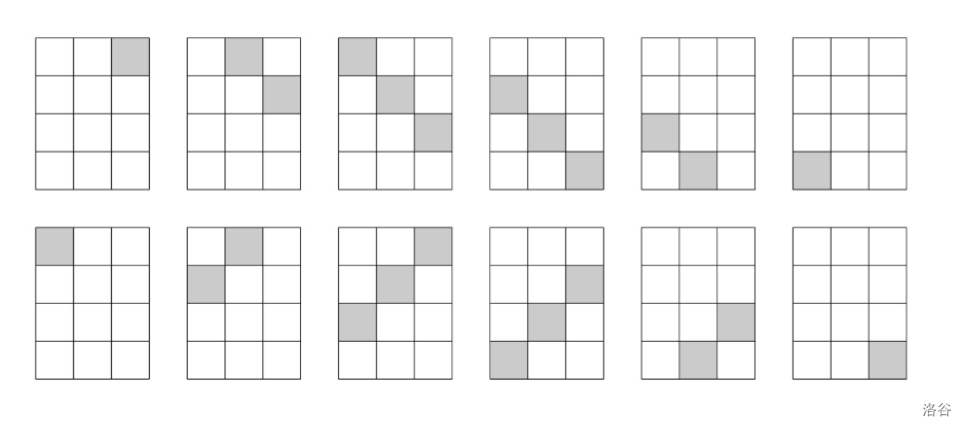
Input Format
The input has $3$ lines.
The first line: two integers $n,m$.
The second line: $m+n-1$ integers describing all diagonals in the $\searrow$ direction. The $1$st integer corresponds to the single cell $(0,n-1)$, the $2$nd integer corresponds to the two cells $(0,n-2),(1,n-1)$, and so on.
The third line: $m+n-1$ integers describing all diagonals in the $\nearrow$ direction. The $1$st integer corresponds to the single cell $(0,0)$, the $2$nd integer corresponds to the two cells $(0,1),(1,0)$, and so on.
Output Format
Output one integer, the answer.
Explanation/Hint
#### Sample Explanation
**Sample 1 Explanation**
- In this case, the following plan can achieve the minimum cost:
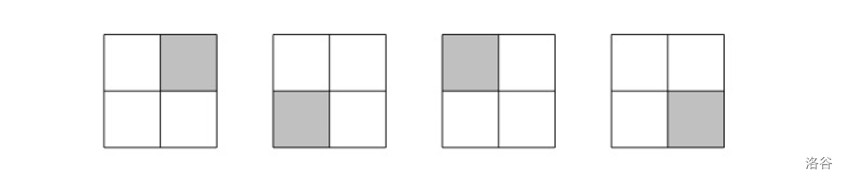
Total cost $=1+1+1+1=4$.
**Sample 2 Explanation**
- In this case, the following plan can minimize the total cost:
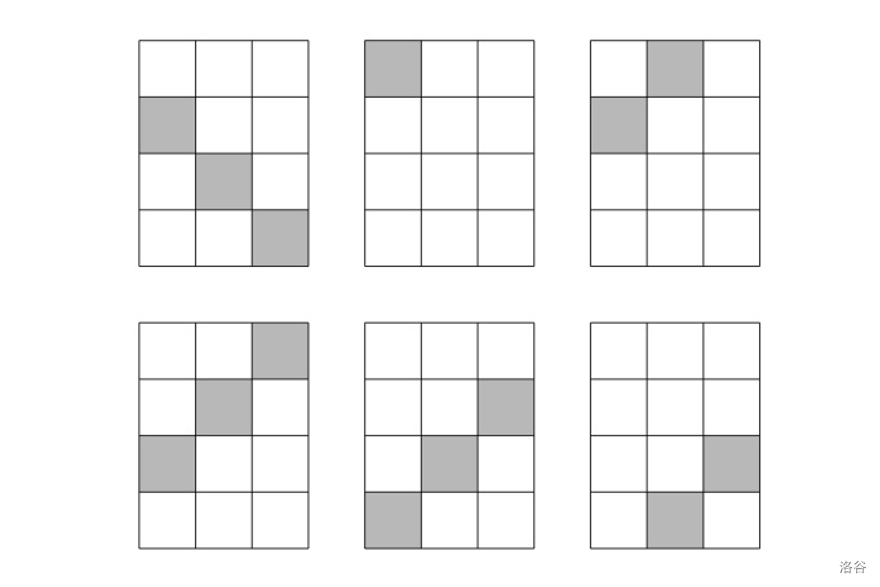
Total cost $=3+2+3+3+1+2=14$.
-------------------------
#### Constraints
**This problem uses bundled subtasks, with $7$ subtasks in total**.
- Subtask 1 (10 points): $n,m\le 4$
- Subtask 2 (10 points): $m,n\le 10$
- Subtask 3 (10 points): $m,n\le 20$
- Subtask 4 (20 points): $m,n\le 2\times 10^3$
- Subtask 5 (10 points): $m=1,n\le 2\times 10^5$
- Subtask 6 (20 points): $m=n\le 2\times 10^5$
- Subtask 7 (20 points): no other constraints.
For all testdata, it is guaranteed that $1\le m,n\le 2\times 10^5$, and the coloring cost of each diagonal is $\in [1,10^9]$.
-----------------------
#### Notes
The original problem is from: [eJOI2019](https://www.ejoi2019.si) Problem E. [Colouring a rectangle](https://www.ejoi2019.si/static/media/uploads/tasks/colouring-isc.pdf).
Translation provided by: @[```_Wallace_```](https://www.luogu.com.cn/user/61430)。
Translated by ChatGPT 5