P6255 [ICPC 2019 WF] Dead-End Detector

### Warning: If you submit a malicious program, you will be banned. ### 警告：恶意提交本题将被封号。

The council of your home town has decided to improve road sign placement,especially for dead ends. They have given you a road map, and you must determine where to put up signs to mark the dead ends. They want you to use as few signs as possible. The road map is a collection of locations connected by two-way streets. The following rule describes how to obtain a complete placement of dead-end signs. Consider a street $S$ connecting a location $x$ with another location. The $x$-entrance of $S$ gets a dead-end sign if, after entering $S$ from $x$, it is not possible to come back to $x$ without making a U-turn. A U-turn is a 180-degree turn immediately reversing the direction. To save costs, you have decided not to install redundant dead-end signs, as specified by the following rule. Consider a street $S$ with a dead-end sign at its $x$-entrance and another street $T$ with a dead-end sign at its $y$-entrance. If, after entering $S$ from $x$, it is possible to go to $y$ and enter $T$ without making a U-turn, the dead-end sign at the $y$-entrance of $T$ is redundant. See Figure E.1 for examples.  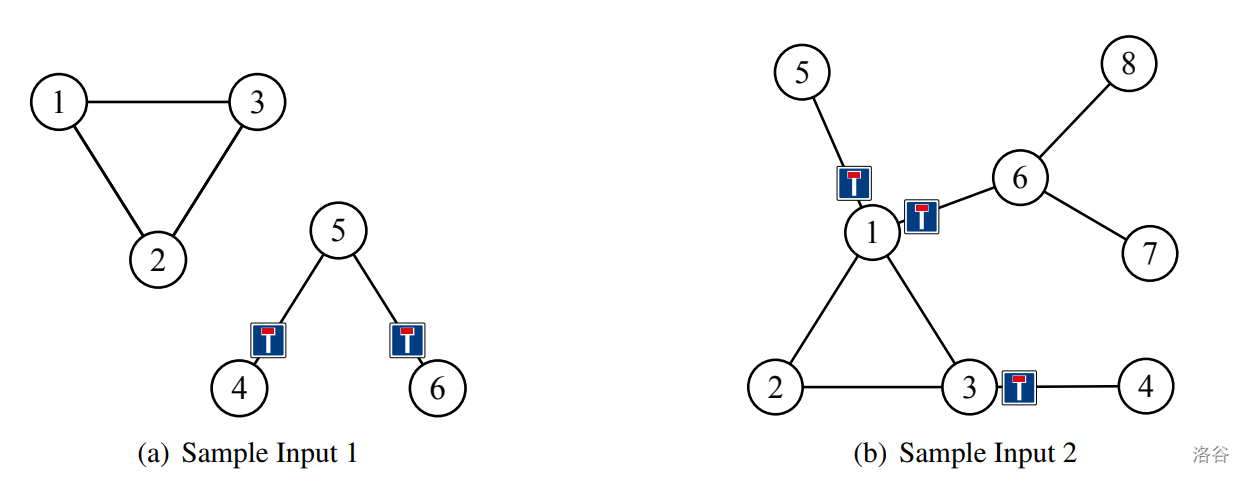Figure E.1: Illustration of sample inputs, indicating where non-redundant dead-end signs are placed.

The first line of input contains two integers $n$ and $m$, where $n$ $(1 \leq n \leq 5\times10^5)$ is the number of locations and $m$ $(0 \leq m \leq 5 \times 10^5)$ is the number of streets. Each of the following $m$ lines contains two integers $v$ and $w$ $(1 \leq v \lt w \leq n)$ indicating that there is a two-way street connecting locations $v$ and $w$. All location pairs in the input are distinct.

On the first line, output $k$, the number of dead-end signs installed. On each of the next $k$ lines, output two integers $v$ and $w$ marking that a dead-end sign should be installed at the $v$-entrance of a street connecting locations $v$ and $w$. The lines describing dead-end signs must be sorted in ascending order of $v$-locations,breaking ties in ascending order of $w$-locations.

Source: ICPC World Finals 2019 Problem E.