P6291 [eJOI 2017] 骆驼
题目描述
我们在棋盘上引入一个新的棋子,称之为“骆驼棋”。棋子跳跃规则:你可以将它移动到水平或垂直方向上的一个位置,使得新位置与旧位置之间隔着 $2$ 格;或者像四个斜对角线的方向之一移动,使得新位置与旧位置之间恰好相隔一个格子。如图,棋盘的中心就是棋子的位置,$8$ 个打上 ”$\times$“标记的就是可以移动到的位置。显然,棋子不可以跳出棋盘。
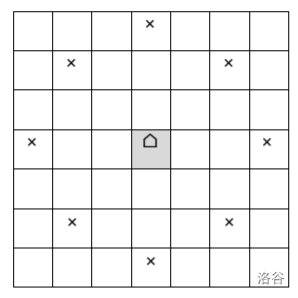
整个棋盘是 $N$ 行 $N$ 列的,其中保证 $5 | N$ 。
一开始,棋子在棋盘的左上角。经过一系列移动,使得整个棋盘每一个格子都被走过恰好一次,并且最后的位置与开始位置之间恰好可以以骆驼棋一步互相到达,这就是所谓的”骆驼循环“。
你需要写一个程序,找到给定棋盘的”骆驼循环”。或者判断是否存在“骆驼循环”。
输入格式
输入仅一行,一个正整数 $N$。
输出格式
首先,如果不存在输出 ```NO```。
输出包含一个 $N \times N$ 的方阵。
方阵包含 $N^2$ 个不同的正整数,大小在 $[1,N^2]$ 范围内,表示每一个格子的访问顺序。那么第一个数字就是 $1$ 。
例如,第 $i$ 行第 $j$ 列的数为 $k$ 说明这一个位置的格子是第 $k$ 个被走到的。详见样例。
说明/提示
#### Special Judge 计分标准
如果可行解有多个,输出任意一个就可以拿到这个测试点的分数。
如果输出不完全或发现不正确的情况你可能会得到一个 UKE。
如果在不该输出 ```NO``` 的地方输出了 ```NO``` ,你们你会得到 ```WA```,以及一句 ```wrong output format Expected integer, but "NO" found```
#### 输入输出样例解释
棋子移动的方式为:$(1,1)$(表示第一行第一列) $\rightarrow (4,1) \rightarrow (7,1) \rightarrow \text{etc.}$
最后棋子在 $(3,3)$ 处停止,恰好可以一步走到起点。
附图:
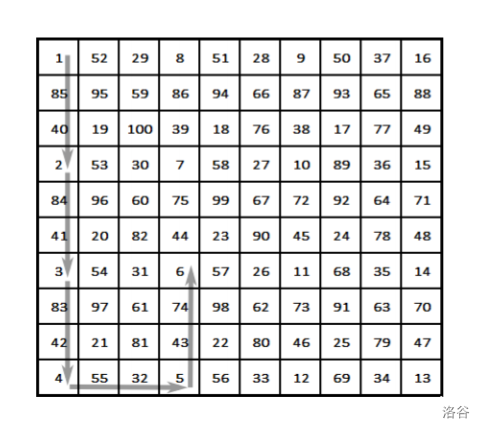
#### 数据规模与约定
对于所有数据,保证 $1\le N\le 10^3$,且 $n$ 是 $5$ 的倍数。
本题共 $17$ 个测试点。
- 对于其中一个测试点,有 $N=5$ ,单点分值比例为 $20 \%$。
- 对于其他 $16$ 个测试点,无其他限制,单点分值比例为 $5\%$。
#### 说明
原题来自:[eJOI2017](www.ejoi.org) Problem D [Camel](http://ejoi.org/wp-content/themes/ejoi/assets/pdfs/tasks_day_2/EN/camel_statement-en.pdf)
翻译提供:@[```_Wallace_```](https://www.luogu.com.cn/user/61430)