P6313 [eJOI 2018] Passports

Gleb is a famous programming teacher from Innopolis. He plans to attend $n$ programming training camps next. Each camp is held in a different country. He has to apply for a visa for each country. For the $i$-th camp, Gleb knows the departure date $s_i$, the duration $len_i$, and the time $t_i$ required to apply for a visa for that country. Gleb has $P$ valid passports, and he needs to decide which passport to use to apply for each visa. For the $i$-th camp, Gleb will leave on the morning of day $s_i$ and return on the evening of day $s_i+len_i-1$. If he applies for a visa on day $d$, Gleb must be in Innopolis at noon that day. This means Gleb cannot apply for a visa during a camp, including the first day and the last day. If one camp ends and Gleb immediately goes to the second camp, he also cannot apply for a visa during that period. The earliest day he can apply for a visa is day $1$. After applying for the visa of the $i$-th country on day $d$, Gleb will receive the passport of that country at noon on day $d+t_i$ (even if Gleb is not in Innopolis on that day). If, on the morning of day $s_i$, Gleb does not have the passport for the corresponding country, he cannot attend the $i$-th camp. **Note that at that moment the passport cannot be inside the embassy processing the visa.** Help Gleb find a visa application plan so that he can attend all the camps successfully.

The first line contains two integers $n, P$, representing the number of camps and the number of passports Gleb has. The next $n$ lines each contain three integers $s_i, len_i, t_i$, representing the start time, duration, and the time required to obtain the visa for the corresponding country for the $i$-th camp. It is guaranteed that the camps do not overlap.

**This problem uses Special Judge**. If there is no plan that allows Gleb to attend all camps, output only `NO`. Otherwise, output `YES` in the first line. Then output $n$ lines. Each line contains two integers: the index of the passport Gleb uses to apply for the visa of that camp’s country, and the day on which he applies for the visa. The output order must match the input order. Days are numbered starting from $1$, and passport indices are $1\cdots P$.

#### Sample Explanation #### Explanation for Sample 1  Each cell represents one day. A rectangle represents a camp: it starts on the morning of some day and ends on the evening of some day. A rectangle with a corner represents a visa application process: it starts at noon of some day and ends at noon of some day. A camp and its corresponding visa application process have the same color. 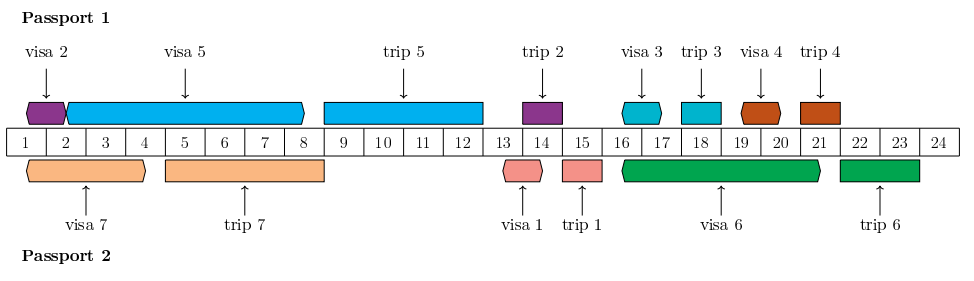#### Explanation for Sample 2  #### Explanation for Sample 3  The above represents the first passport, and the below represents the second passport. --- #### Constraints and Notes **This problem uses bundled testdata with 9 subtasks**. - Subtask 1 (5 pts): $n\leq 2$, $s_i,len_i,t_i\leq 100$, all $t_i$ are equal, $P=1$; - Subtask 2 (8 pts): $n\leq 10$, $s_i,len_i,t_i\leq 100$, all $t_i$ are equal, $P=1$; - Subtask 3 (7 pts): $n\leq 10$, $s_i,len_i,t_i\leq 100$, all $t_i$ are equal; - Subtask 4 (12 pts): $n\leq 16$, $s_i,len_i,t_i\leq 100$, $P=1$; - Subtask 5 (13 pts): $n\leq 16$, $s_i,len_i,t_i\leq 100$; - Subtask 6 (15 pts): $n\leq 18$, $s_i,len_i,t_i\leq 10^7$, $P=1$; - Subtask 7 (15 pts): $n\leq 18$, $s_i,len_i,t_i\leq 10^7$; - Subtask 8 (15 pts): $n\leq 20$; - Subtask 9 (10 pts): no special constraints. For all testdata, it is guaranteed that $1\leq n\leq 22$, $1\leq P\leq 2$, $1\leq s_i,len_i,t_i\leq 10^9$. --- Source: [eJOI2018](http://ejoi2018.org/) Problem B "Passports". Note: Translated by myself. Translated by ChatGPT 5