P6343 [CCO 2017] The Rise of the Rectangular Empire

A long, long time ago, the Rectangular Empire ruled the Cartesian Continent. The empire was rich and powerful, and through endless wars and conquests, its territory expanded day by day. The Rectangular Empire used a **rectangular district system**. These districts all satisfy three special rules. 1. The empire’s territory is divided into districts, and every piece of land belongs to one and only one district. 2. When viewed on the map, each district must be a rectangle, and the longer side must be twice the length of the shorter side. 3. The side lengths of each district must be integers, measured in $Ξ$ ($Ξ$ is the empire’s unit of measurement). When the empire was first founded, it consisted of a single district. From then on, to expand its land, the empire continuously conquered neighboring areas. Each time the empire gained control of a new area, it always created a separate new district that occupies all of the newly acquired land. This means the empire only cares about the geometric properties of the land it wants to conquer. You may assume that no two conquests happen at the same location. The empire can expand only by adding new districts. Also, once a district is added, it is never modified or merged with another one. The final rule of the Rectangular Empire is to ensure that the empire’s overall shape is a rectangle. However, the aspect ratio of this large rectangle does not need to be $2:1$. The empire has length $n$ and width $m$ (in units of $Ξ$). Your task is to estimate the number of districts the empire can have for an $n \times m$ empire. Among all possible cases, what are the minimum and maximum possible numbers of districts?

The input contains a single line with two integers $n, m$.

Output a single line with two integers. The first is the minimum number of districts, and the second is the maximum number of districts.

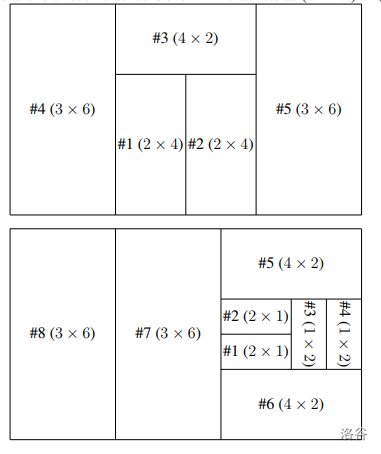
#### Sample Explanation  #### Constraints and Notes **This problem uses bundled testdata with a total of $3$ subtasks.** - Subtask 1 (20 points): $1 \le n,m \le 10^3$. - Subtask 2 (32 points): $1 \le n,m \le 10^6$. - Subtask 3 (48 points): $1 \le n,m \le 10^8$. For all testdata, it is guaranteed that $1 \le n,m \le 10^8$. Source: [CCO 2017](https://cemc.math.uwaterloo.ca/contests/computing/2017/index.html) Day 1 “[Cartesian Conquest](https://cemc.math.uwaterloo.ca/contests/computing/2017/stage%202/day1.pdf)”. Note: This translation is from [LOJ](https://loj.ac/problem/2751). Translated by ChatGPT 5