P6343 [CCO 2017] 矩形帝国的霸业

很久很久以前，矩形帝国统治了笛卡尔大陆。帝国繁荣昌盛，在无尽的战争与征服之中，帝国的土地一天天扩大。 矩形帝国实行 **矩形区域制**。这些地区都满足三个特殊标准。 1. 帝国的领土被划分为各个地区，且每一片土地属于且只属于一个地区； 2. 在地图上观察时，每个区域的形状必须是矩形且长边的长度是短边长度的两倍； 3. 区域各边的长度必须是整数，以 $Ξ$ 为单位（$Ξ$ 是矩形帝国的计量单位）。 帝国最初建立的时候，它由一个单一的区域组成。从那时起，为了扩充疆域，帝国会不断征服邻近区域。每当帝国控制一个新的区域时，他们总是建立一个独立的新区域，新区占用刚获得的全部土地。这意味的帝国只在乎他们想要征服的土地的几何属性。你可以假设没有两次征服出现在同一个地方。 帝国只能通过增加新区来扩充疆域。此外，每个地区一旦添加，就不会被修改或和另外一个合并。 矩形帝国的最后一个标准，是确保帝国的整体形状是一个矩形。不过，大矩形的长宽比可以不满足 $2:1$。 帝国的长度是 $n$，宽度是 $m$（以 $Ξ$ 为单位）。你的任务是估计在 $n \times m$ 的大小下帝国的区域数。在所有可能的情况下，帝国的最小区域数和最大区域数分别是什么？

输入只有一行两个整数，分别为 $n,m$。

输出只有一行两个整数，第一个是最小的区域数，第二个是最大的区域数。

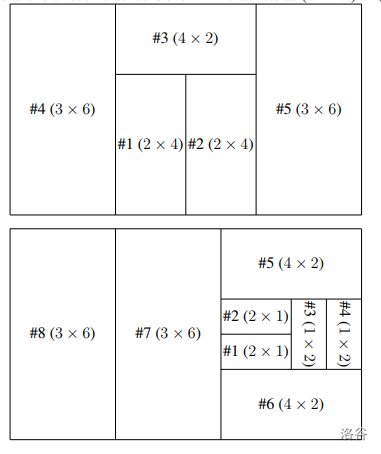
#### 样例解释  #### 数据范围及约定 **本题采用多测试点捆绑测试，共有 $3$ 个子任务。** - Subtask 1（20 points）：$1 \le n,m \le 10^3$； - Subtask 2（32 points）：$1 \le n,m \le 10^6$； - Subtask 3（48 points）：$1 \le n,m \le 10^8$。 对于全部的测试点，保证 $1 \le n,m \le 10^8$。 来源：[CCO 2017](https://cemc.math.uwaterloo.ca/contests/computing/2017/index.html) Day1「[Cartesian Conquest](https://cemc.math.uwaterloo.ca/contests/computing/2017/stage%202/day1.pdf)」。 说明：翻译来自 [LOJ](https://loj.ac/problem/2751)。