P6344 [CCO 2017] Vera and Modern Art

Inspired by the great painter Picasso, Vera decided to create her masterpiece. She has a canvas that can be simplified as an infinitely large 2D plane. Vera likes integer powers of $2$ $(1,2,4,8,16,\ldots)$, and she will color some points using step sizes that are powers of $2$. Vera will color $n$ times. The $i$-th coloring operation is described by three integers $x_i, y_i, v_i$. Let $a_i$ be the largest power of $2$ that is not greater than $x_i$, and let $b_i$ be the largest power of $2$ that is not greater than $y_i$. Vera will use color $v_i$ to color all points with coordinates $(x_i + a_i p, y_i + b_i q)$, where $p, q$ are non-negative integers. A point may be colored multiple times with different colors, and it may also be colored multiple times with the same color. The color value of a point is the sum of all colors that have been applied to that point. Then Vera will ask $Q$ questions. For the $j$-th question, she wants to know the color value of the point at coordinates $(r_j, c_j)$. If a point has never been colored, then its color value is $0$. Because you are forced to be Vera's assistant, you have to answer Vera's questions.

The first line contains two integers $n, Q$, separated by a space. The next $n$ lines each contain three integers $x_i, y_i, v_i$ separated by spaces, meaning that the coloring operation described in the statement is performed using color $v_i$, with parameters $x_i$ and $y_i$. The next $Q$ lines each contain two integers $r_j, c_j$ separated by spaces, asking for the color value of the point $(r_j, c_j)$.

Output $Q$ lines. Each line contains one integer. The integer on the $j$-th line is the color value of the point $(r_j, c_j)$.

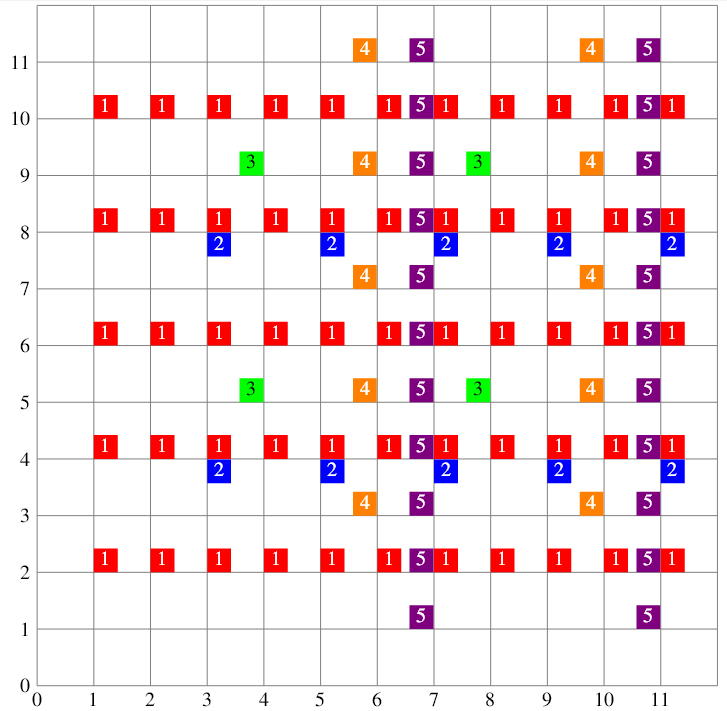
#### Sample Explanation Let colors $1,2,3,4,5$ be red, blue, green, orange, and purple, respectively. Let $p, q$ be non-negative integers. Then: - Points with coordinates $(1 + p, 2 + 2q)$ are colored red. - Points with coordinates $(3 + 2p, 4 + 4q)$ are colored blue. - Points with coordinates $(4 + 4p, 5 + 4q)$ are colored green. - Points with coordinates $(6 + 4p, 3 + 2q)$ are colored orange. - Points with coordinates $(7 + 4p, 1 + q)$ are colored purple. The coordinate grid from $(0,0)$ to $(11,11)$ is shown in the figure: We can observe that: - $(2,6)$ is colored red, so its color value is $1$. - $(7,8)$ is colored red, blue, and purple, so its color value is $1+2+5=8$. - $(5,9)$ is not colored, so its color value is $0$. - $(11,2)$ is colored red and purple, so its color value is $1+5=6$. - $(10,7)$ is colored orange, so its color value is $4$. - $(4,5)$ is colored green, so its color value is $3$.  #### Constraints and Notes - For $20\%$ of the testdata, $1 \le n, Q \le 2 \times 10^3$. - For another $20\%$ of the testdata, $y_i = 1 \ (1 \le i \le n)$. - For another $20\%$ of the testdata, $1 \le n, Q \le 10^5$ and $1 \le r_j, c_j \le 10^9 \ (1 \le j \le Q)$. - For $100\%$ of the testdata, $1 \le n, Q \le 2 \times 10^5$, $1 \le i \le n$, $1 \le v_i \le 10^4$, $1 \le x_i, y_i, r_j, c_j \le 10^{18}$, and $1 \le j \le Q$. Due to issues with the judging machine, only the last $10$ test cases are kept. Source: [CCO 2017](https://cemc.math.uwaterloo.ca/contests/computing/2017/index.html) Day 1 “ [Vera and Modern Art](https://cemc.math.uwaterloo.ca/contests/computing/2017/stage%202/day1.pdf) ”. Note: This translation is from [LOJ](https://loj.ac/problem/2752). Translated by ChatGPT 5