P6350 [PA 2011] Laser Pool

在一个 $n\times m$ 的网格（左下角为 $(1,1)$，右上角为 $(m,n)$）里有一个小球（可以视为一个点），其中横向和纵向都有一些光线，$q$ 次询问，每次给出小球的初始位置，方向，速度和运动时间（具体方式见输入格式），求出小球触碰光线的次数，如果碰到交点只算一次。 当小球触碰到边界时，会发生反弹，也就是说，假设当前每秒 $x$ 坐标增加 $vx$，$y$ 增加 $vy$，如果碰到上下边界，则 $vy$ 变为 $-vy$，如果碰到左右边界，将 $vx$ 变为 $-vx$，如果仍不理解可以见样例解释的图片。

第一行两个整数 $n,m$，表示网格的行数和列数。 接下来一行一个长为 $n$ 的 $01$ 串，如果第 $i$ 个数为 $1$，则表示这一行有光线，否则表示没有。 接下来一行一个长为 $m$ 的 $01$ 串，如果第 $i$ 个数为 $1$，则表示这一列有光线，否则表示没有。 接下来一行一个数 $q$，表示询问次数。 下面 $q$ 行，每五个整数 $x,y,vx,vy,t$ 表示小球初始时在 $(x,y)$，每秒 $x$ 增加 $vx$，$y$ 坐标增加 $vy$，总共运动 $t$ 秒。保证 $vx,vy$ 均为 $1$ 或 $-1$。

对于每一次询问，输出一行一个数，表示小球触碰光线的次数。

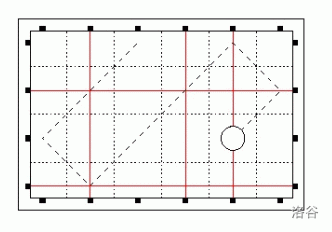
 $1\leq n,m\leq 10^5$，$1\leq q\leq 10^4$，$1\leq t \leq 10^9$，保证球的初始位置在网格内且不在边界上，$vx,vy$ 均为 $1$ 或 $-1$。