P6350 [PA 2011] Laser Pool

In an $n \times m$ grid (with the bottom-left corner at $(1,1)$ and the top-right corner at $(m,n)$), there is a small ball (which can be treated as a point). Some rows and some columns contain laser beams. There are $q$ queries. Each query gives the ball’s initial position, direction, speed, and travel time (see the input format for details). You need to find how many times the ball touches a laser beam. If it touches an intersection point of a row-beam and a column-beam, it is counted only once. When the ball touches the boundary, it reflects. That is, suppose the current change per second is that the $x$ coordinate increases by $vx$ and the $y$ coordinate increases by $vy$. If it hits the top or bottom boundary, then $vy$ becomes $-vy$. If it hits the left or right boundary, then $vx$ becomes $-vx$. If this is still unclear, refer to the picture in the sample explanation.

The first line contains two integers $n,m$, representing the number of rows and columns of the grid. The next line is a binary string of length $n$. If the $i$-th character is $1$, then row $i$ has a laser beam; otherwise, it does not. The next line is a binary string of length $m$. If the $i$-th character is $1$, then column $i$ has a laser beam; otherwise, it does not. The next line contains an integer $q$, representing the number of queries. The following $q$ lines each contain five integers $x,y,vx,vy,t$, meaning that initially the ball is at $(x,y)$. Each second, $x$ increases by $vx$ and $y$ increases by $vy$, and it moves for a total of $t$ seconds. It is guaranteed that $vx,vy$ are both $1$ or $-1$.

For each query, output one number per line, representing the number of times the ball touches a laser beam.

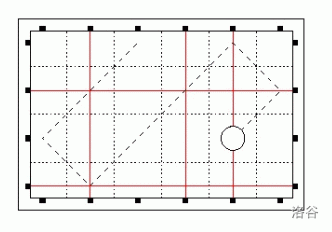
 Constraints: $1 \leq n,m \leq 10^5$, $1 \leq q \leq 10^4$, $1 \leq t \leq 10^9$. It is guaranteed that the ball’s initial position is inside the grid and not on the boundary, and $vx,vy$ are both $1$ or $-1$. Translated by ChatGPT 5