P6362 Euclidean Minimum Spanning Tree on a Plane

2025/06/13 @[ケロシ](https://www.luogu.com.cn/user/511639) added ten sets of hack testdata, located in Subtask 1.

There are $n$ points on a plane. The coordinates of point $i$ are $(x_i, y_i)$. The edge weight between points $i$ and $j$ is $\sqrt{(x_i - x_j) ^ 2 + (y_i - y_j) ^ 2}$. Find the sum of edge weights of the minimum spanning tree.

The first line contains an integer $n$. The next $n$ lines each contain two integers $x_i, y_i$.

Output one line with a real number, representing the answer. Your output will be considered correct if the absolute error or relative error compared to the standard output is within $10^{-6}$.

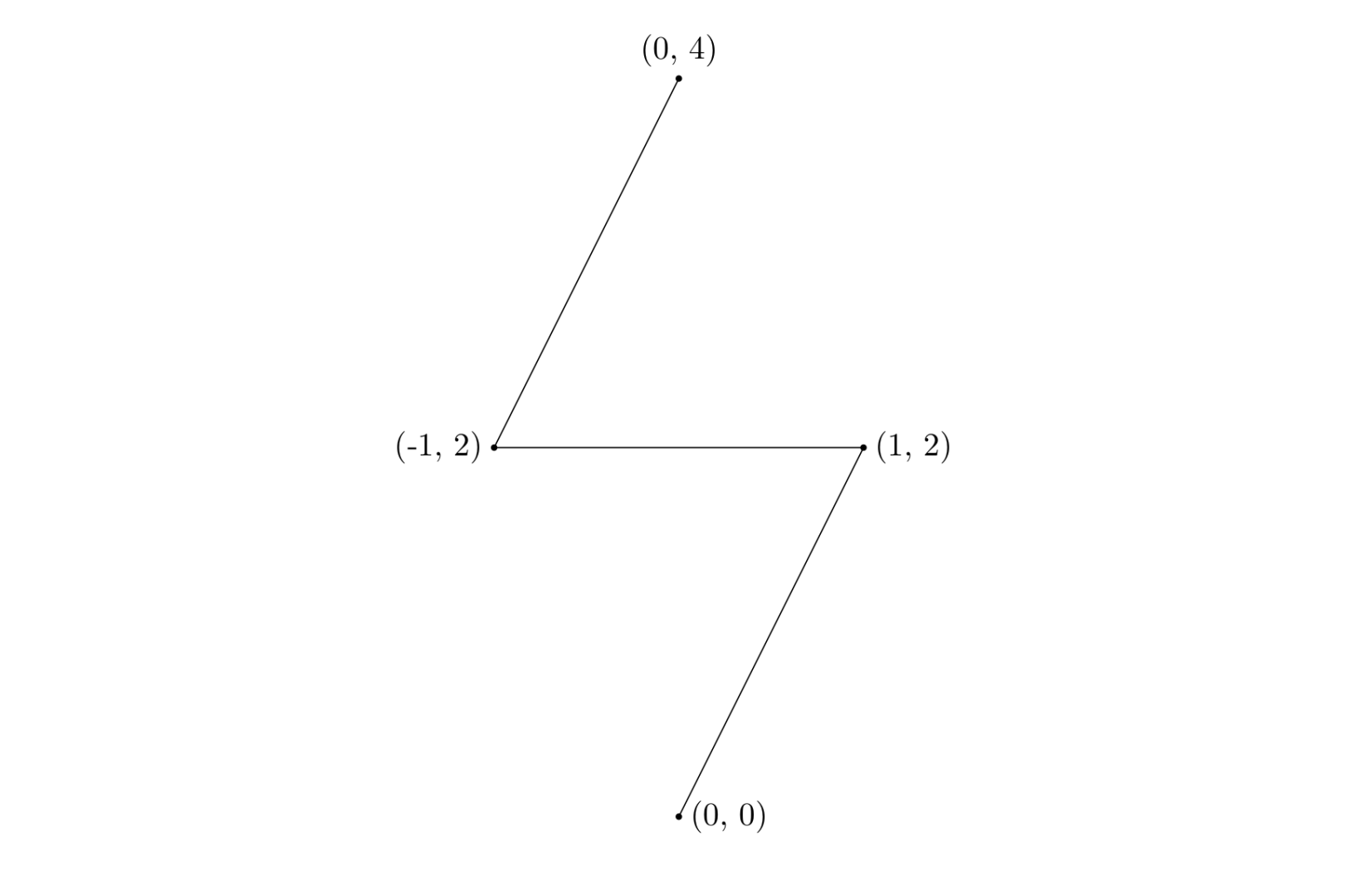
#### Sample Explanation 1 In this sample, the minimum spanning tree is shown in the figure below:  The sum of edge weights is $2 \sqrt{5} + 2 \approx 6.47213595500$. --- #### Constraints - For $50\%$ of the testdata, $n \le 5000$. - For $100\%$ of the testdata, $3 \le n \le 10 ^ 5$, $\lvert x_i \rvert$, $\lvert y_i \rvert \le 10 ^ 5$. Translated by ChatGPT 5