P6374 「StOI-1」树上询问
题目描述
给定一棵 $n$ 个点的无根树,有 $q$ 次询问。
每次询问给一个参数三元组 $(a,b,c)$ ,求有多少个 $i$ 满足这棵树在以 $i$ 为根的情况下 $a$ 和 $b$ 的 [LCA](https://www.luogu.com.cn/problem/P3379) 为 $c$ 。
输入格式
第一行 $2$ 个数,为 $n$ 和 $q$ 。
接下来 $n-1$ 行,每行 $2$ 个数,表示树的一条边。
接下来 $q$ 行,每行 $3$ 个数,为 $(a,b,c)$。
输出格式
共 $q$ 行,每行一个数,为对于每个三元组的 $i$ 的个数。
说明/提示
---
#### 样例 2 解释
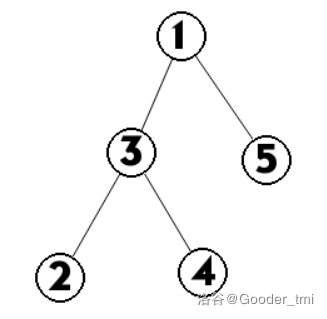
第一个查询的 $i$ 为 3 和 4。
第二个查询的 $i$ 为 1。
---
#### 数据范围
#### 本题按子任务测试:
$subtask1 (20pts)$:$1 \leq n \leq$ $1000$ ,$1 \leq q \leq$ $500$ 。
$subtask2 (15pts)$:$1 \leq n \leq$ $10^{5}$,$1 \leq q \leq$ $10^{5}$,树退化成链 。
$subtask3 (25pts)$:$1 \leq n \leq$ $5$ $\times$ $10^{5}$,$1 \leq q \leq $ $10^{5}$,数据**不随机** 。
$subtask4 (40pts)$:$1 \leq n \leq$ $5$ $\times$ $10^{5}$,$1 \leq q \leq $ $2$ $\times$ $10^{5}$ 。
对于所有数据:$1 \leq n \leq$ $5$ $\times$ $10^{5}$,$1 \leq q \leq $ $2$ $\times$ $10^{5}$ 。
注:数据强度不高,不必卡常与快读快输。