P6399 [COI 2008] TAMNICA

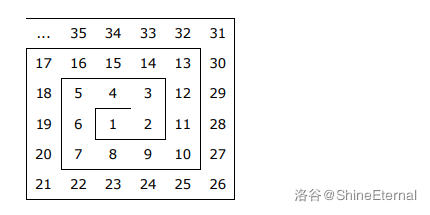
 There is an infinite maze where the numbers are arranged as shown in the figure. A black line between two numbers means there is a wall separating them; if there is no line, then you can move between them. You start from $1$, and the exit is at $n$. Now, because of an earthquake, some walls have collapsed, which makes it easier for you to move around. Taking advantage of the chaos, you need to escape as fast as possible by passing through as few numbers as you can. Please compute the minimum number of steps needed to escape.

The first line contains an integer $n$, which indicates the cell where the exit is located. The second line contains an integer $k$, which indicates the number of walls that collapsed due to the earthquake. The next $k$ lines each contain an integer $b$, meaning the number on one side of a collapsed wall. The number $a$ on the other side is not given, but it is known that $a

Output one integer in one line, indicating the minimum number of numbers that need to be passed through (not including $1$).

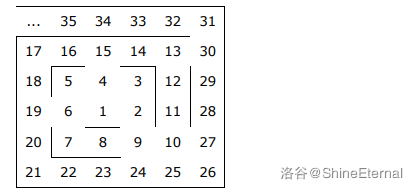
#### Explanation for Sample 1  The state of the maze after the earthquake for Sample $1$ is shown in the figure. The route $1-4-15-14-13-30-31$ escapes the fastest. A total of $6$ numbers are passed through. #### Constraints - For $50\%$ of the testdata, $n\le 10^6$. - For $100\%$ of the testdata, $1\le n\le 10^{15}$, $1\le k\le 10^5$, $4\le b\le 10^{15}$. #### Note **Translated from [COCI2007-2008](https://hsin.hr/coci/archive/2007_2008/) [COI2008](https://hsin.hr/coci/archive/2007_2008/olympiad_tasks.pdf) *T3 TAMNICA***。 Translated by ChatGPT 5