P6404 [COCI 2014/2015 #2] BOB

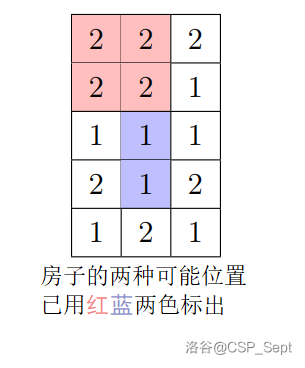
Bob 是一位著名的建设者。他买了地，想盖房子。不幸的是，问题是土地的地形，土地不同地方的海拔不一定一样。 这块地呈长方形，宽 $n$ 米，长 $m$ 米。它可以分为 $n\times m$ 个方格（见图片）。Bob 的房子将被塑造成一个长方形，它的边与土地的边平行，其顶点与正方形的顶点重合。Bob 的房子所覆盖的所有土地必须具有相同的高度，以防倒塌。  请计算出 Bob 建房的方法数。 **形式化地**，求出一个矩阵中所有元素均相等的子矩阵个数。

第一行输入包含整数 $n$ 和 $m$。 以下 $n$ 行中的每一行都包含 $m$ 个整数 $a_{i,j}$，分别是每平方土地的海拔高度。 **由于输入量很大，请使用更快的输入方法。**

仅一行，即 Bob 建房的方法数。

#### 样例 1 说明 一些可能的房屋位置是分别以 $(0,0)-(1,1),(0,0)-(0,2)$ （高度为 $2$）$(2,0)-(2,2),(1,2)-(2,2)$（高度为 $1$）为左上角顶点和右下角顶点的矩形。括号中的第一个数字表示行号，第二个数字表示列号（坐标以 $0$ 开始）。 #### 数据规模与约定 - 对于 $20\%$ 的数据，有 $1\le n,m\le 50$。 - 对于 $60\%$ 的数据，有 $1\le n,m\le 500$。 - 对于 $100\%$ 的数据，有 $1\le n,m\le 10^3$。 对于所有合法的 $a_{i,j}$，都有 $1\le a_{i,j}\le 10^9$。 #### 说明 **题目译自 [COCI2014-2015](https://hsin.hr/coci/archive/2014_2015/) [CONTEST #2](https://hsin.hr/coci/archive/2014_2015/contest2_tasks.pdf) _T4 BOB_。**