P6404 [COCI 2014/2015 #2] BOB

Bob is a famous builder. He bought some land and wants to build a house. Unfortunately, the problem is the terrain: the elevation may not be the same at different places on the land. The land is a rectangle, with width $n$ meters and length $m$ meters. It can be divided into an $n \times m$ grid of cells (see the picture). Bob’s house will be shaped as a rectangle whose sides are parallel to the sides of the land, and whose vertices coincide with grid vertices. All the land covered by Bob’s house must have the same height, so that it will not collapse.  Compute the number of ways Bob can build his house. **Formally**, find the number of submatrices in a matrix whose elements are all equal.

The first line contains integers $n$ and $m$. Each of the next $n$ lines contains $m$ integers $a_{i,j}$, the elevation height of each unit square of land. **Since the input is very large, please use a faster input method.**

Output a single line: the number of ways Bob can build his house.

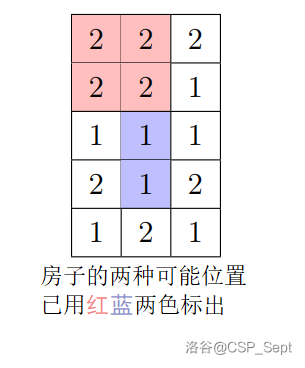
#### Explanation for Sample 1 Some possible house positions are the rectangles with top-left and bottom-right vertices at $(0,0)-(1,1)$ and $(0,0)-(0,2)$ (height $2$), and $(2,0)-(2,2)$ and $(1,2)-(2,2)$ (height $1$). The first number in the parentheses is the row index and the second number is the column index (coordinates start from $0$). #### Constraints - For $20\%$ of the testdata, $1 \le n, m \le 50$. - For $60\%$ of the testdata, $1 \le n, m \le 500$. - For $100\%$ of the testdata, $1 \le n, m \le 10^3$. For all valid $a_{i,j}$, $1 \le a_{i,j} \le 10^9$. #### Note **This problem is translated from [COCI2014-2015](https://hsin.hr/coci/archive/2014_2015/) [CONTEST #2](https://hsin.hr/coci/archive/2014_2015/contest2_tasks.pdf) _T4 BOB_.** Translated by ChatGPT 5