P6407 [SDOI2012] Chessboard Covering
Description
On an $n \times m$ chessboard, there are $K$ cells called special cells. We want to use a set of Tetris pieces to cover the chessboard, ensuring that special cells cannot be covered, and each non-special cell can be covered by only one Tetris piece. Find the maximum number of Tetris pieces that can be placed.
It is known that there are the following three sets of Tetris pieces, and a chessboard will use one of these sets.
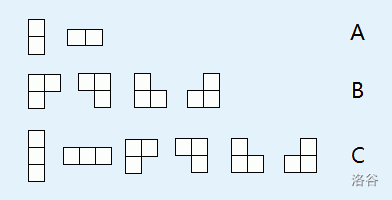
Input Format
The first line contains three integers $n, m, K$ and a character `type`, which indicates the set of Tetris pieces used.
The next $K$ lines each contain two integers $x, y$, meaning that the cell in row $x$ and column $y$ is a special cell.
Output Format
Output one integer, the required answer.
Explanation/Hint
For test points $1 \sim 6$, $1 \le n, m \le 100$, $0 \le K \le nm$, and `type` is `A`.
For test points $7 \sim 12$, $2 \le n = m \le 2^{2 \times 10^5}$, $n, m$ are integer powers of $2$, $K = 1$, and `type` is `B`.
For test points $13 \sim 21$, $1 \le n, m \le 11$, $0 \le K \le nm$, and `type` is `C`.
Translated by ChatGPT 5