P6410 [COCI 2008/2009 #3] CROSS

在数独游戏中，目标是将 $1 \sim 9$ 的整数放入 $9 \times 9$ 网格中，这样每行每列以及 $9$ 个 $3 \times 3$ 框的每一个都包含所有 $9$ 个数字不重复的数字。开始 $9 \times 9$ 的方格纸已部分填充，因此可以从逻辑上推导出其他单元格的值。 数独有很多难题，解决越困难的往往需要越复杂的分析方法。

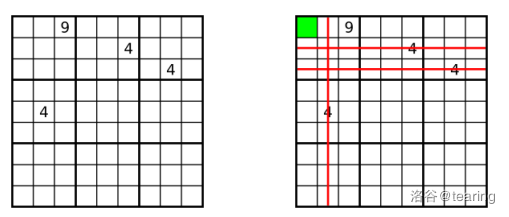
在这道题中，你需要用到最简单的方法，即交叉影线。 在方格之中，我们选择 $9$ 个数字中的 $1$ 个，并针对网格中每个出现的数字划掉相应的行，列和 $3 \times 3$ 的框。 寻找一个的 $3 \times 3$ 区域，将号码的位置并将其放置在此处。 系统会为您提供部分填充的网格。您的任务是重复使用交叉影线的方法，对于不同的数字，直到无法再对任何数字进行推论。 下面的第一张图片显示了一个非常稀疏的数独。但是，即使如此稀疏，但在此网格中仍然可以使用交叉阴影线推断左上角单元格中的数字为 $4$，如第二张图片。  另外，在下列情况下，您需要输出 $\tt ERROR$： - 数字在网格中的初始放置无效。 - 在所有的 $3 \times 3$ 框中无法填写此数字。

输入有 $9$ 行，每行 $9$ 个字符。每个字符将是一个在 $1$ 到 $9$ 之间，或是一个 $\tt .$，表示空。

如果输入有效且求解时没有矛盾，则应在相同的位置输出网格给出的格式。 如果可以使用交叉阴影线推导出其值，则填充单元格。 否则输出 $\tt ERROR$。

#### 说明 **题目译自 [COCI2008-2009](https://hsin.hr/coci/archive/2008_2009/) [CONTEST #3](https://hsin.hr/coci/archive/2008_2009/contest3_tasks.pdf) *T3 CROSS*。**