P6410 [COCI 2008/2009 #3] CROSS

In the Sudoku game, the goal is to place the integers $1 \sim 9$ into a $9 \times 9$ grid so that each row, each column, and each of the $9$ $3 \times 3$ boxes contains all $9$ digits with no repetition. The initial $9 \times 9$ grid is partially filled, so the values of other cells can be logically deduced. There are many difficult Sudoku puzzles, and the harder ones often require more complex analysis methods.

In this problem, you need to use the simplest method, namely cross-hatching. In the grid, we choose one digit among the $9$ digits, and for every occurrence of this digit in the grid, we cross out the corresponding row, column, and $3 \times 3$ box. Find a $3 \times 3$ box where the position of this digit can be determined, and place it there. The system will give you a partially filled grid. Your task is to repeatedly use the cross-hatching method for different digits, until no further deduction can be made for any digit. 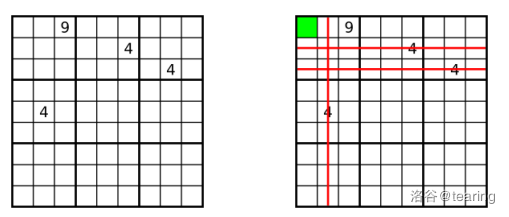The first picture below shows a very sparse Sudoku. However, even though it is so sparse, in this grid you can still use cross-hatching to deduce that the digit in the top-left cell is $4$, as shown in the second picture.  In addition, you need to output $\tt ERROR$ in the following cases: - The initial placement of digits in the grid is invalid. - For some digit, it cannot be placed in any of the $3 \times 3$ boxes.

The input consists of $9$ lines, each containing $9$ characters. Each character is either a digit from $1$ to $9$, or $\tt .$ indicating an empty cell.

If the input is valid and there is no contradiction during solving, output the grid in the same format as the input. Fill in the cells whose values can be deduced using cross-hatching. Otherwise, output $\tt ERROR$.

#### Note **This problem is translated from [COCI2008-2009](https://hsin.hr/coci/archive/2008_2009/) [CONTEST #3](https://hsin.hr/coci/archive/2008_2009/contest3_tasks.pdf) *T3 CROSS*.** Translated by ChatGPT 5