P6429 [COCI 2008/2009 #1] JEZ

There is a rectangle of height $r$ and width $c$, divided into $r \times c$ small $1 \times 1$ rectangles. **Rows are numbered from top to bottom from $0$ to $r-1$, and columns are numbered from left to right from $0$ to $c-1$.** Each small rectangle has a color. If a small rectangle is at row $x$ and column $y$, then: - If $x\oplus y=x+y$, this rectangle is gray. - Otherwise, it is white. 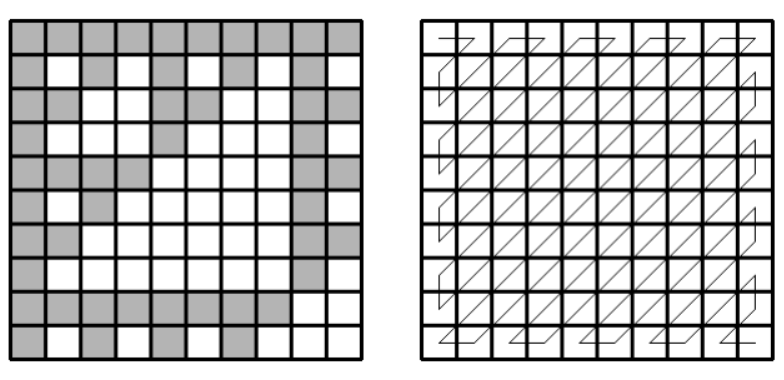The lower-left figure shows the case $r=c=10$:  Now someone walks $k$ steps along the path shown in the upper-right figure on this rectangle. Find how many gray cells they step on.

The first line contains two integers $r$ and $c$. The second line contains one integer $k$.

Output one line containing the number of gray cells they step on.

#### Constraints - For $50\%$ of the testdata, $k\le 10^6$ is guaranteed. - For $100\%$ of the testdata, $1\le r,c\le 10^6$, $1\le k\le r\times c$, and the answer fits in a $32$-bit integer. #### Notes: #### This problem is translated from [COCI2008-2009](https://hsin.hr/coci/archive/2008_2009/) [CONTEST #1](https://hsin.hr/coci/archive/2008_2009/contest1_tasks.pdf) JEZ. Translator: @[菜鸟一只](https://www.luogu.com.cn/user/175829)。 Translated by ChatGPT 5