P6455 Invisible Boundary Line [Ring Version]

- Original problem: [P5617 [MtOI2019]Invisible Boundary Line](https://www.luogu.com.cn/problem/P5617). **Appendix**: [Some information about this problem’s `SPJ` and testdata](https://www.luogu.com.cn/paste/tmwvh5vh). If there are issues such as precision hacks, broken testdata, or cases that beat the intended solution, please contact the problem setter.

There are $n$ circles with radius $r$, drawn on a paper ring of length $L$ whose ends are connected. All circle centers are at the same height. You can think of drawing a number line on the paper and then rolling it up; the positions of the centers are described by points on this number line. If you cannot understand how the circles are distributed on the ring, please refer to the sample explanation and subtasks. You need to choose $k$ circles so that the area of the union of all chosen circles is maximized. Note that you must output an exact selection scheme, not just the maximum union area.

The first line contains four integers $n, k, r, L$, with meanings as described in the statement. The second line contains $n$ integers. The $i$-th integer $p[i]$ describes the position of the $i$-th circle center on the paper ring (the coordinate on the number line). For $2

Output one line containing $k$ integers, representing the indices of the circles you selected. The `SPJ` will compute the union area. You must ensure these indices are strictly increasing and within $[1,n]$. Otherwise, it is considered invalid and you will receive no score. It is considered correct if the **relative error** compared to the standard answer does not exceed $10^{-9}$, and the **absolute error** does not exceed $0.1$. By estimation, the answer will not exceed the order of magnitude $10^{12}$.

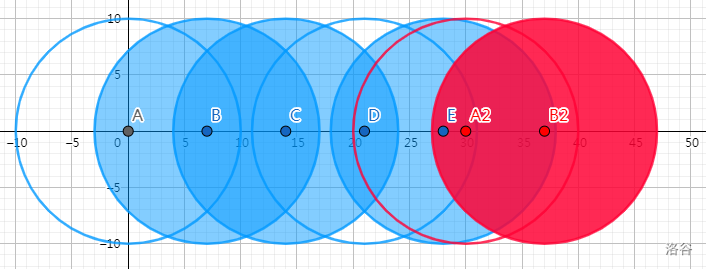
**Sample Explanation**: - **Sample 1**: The final union area is approximately $565.871835$. The distribution of circles is shown in the figure. Here, $⊙A$ and $⊙A2$ are the same circle, and $⊙B$ and $⊙B2$ are the same circle. This can be viewed as shifting to the right by $L = 30$ units. In fact, this is equivalent to making a full round on the paper ring and returning to the start. Since they are the same circle, the area covered by the red part cannot be counted repeatedly. The maximum union area is the blue part.  - **Sample 2**: The final union area is approximately $942.477796$. - **Sample 3**: The final union area is approximately $16817.058547$. **Constraints and Conventions**: | Subtask ID | n | k | Time Limit | | :--: | :--: | :--: | :--: | | 1 | $10$ | - | $\texttt{1s}$ | | 2 | $100$ | - | $\texttt{1s}$ | | 3 | $2000$ | - | $\texttt{1.6s}$ | | 4 | $3\times 10^4$ | $100$ | $\texttt{2.2s}$ | | 5 | $1\times 10^5$ | - | $\texttt{3s}$ | The time limit is more than twice the running time of `std`. For all testdata, $n \leq 10^5$, $10 \leq r \leq 2000$, $0 \leq p[i] < L \leq 10^8$, $4r < L$, $3 \leq k \leq n$. All values in the table are upper bounds. Note that some lower-bound restrictions may help remove certain boundary cases. Translated by ChatGPT 5