P6480 [CRCI2006-2007] TETRIS

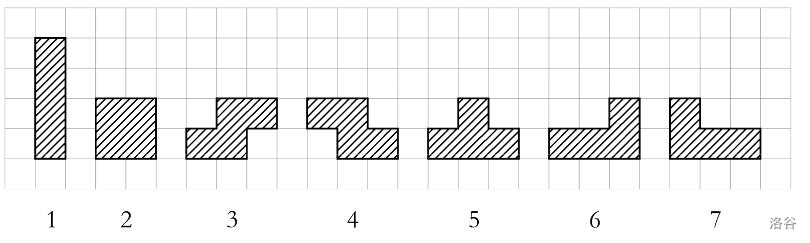
There are the following seven types of Tetris blocks:  When using them, you may rotate them by $90$ degrees, $180$ degrees, $270$ degrees, or not rotate them. Now there is a grid with $n$ columns and unlimited height. In the $i$-th column, the bottom $a_i$ cells are already filled with blocks (that is, the lowest $a_i$ cells have been placed previously). In each column, only a continuous segment of cells at the bottom is filled. The next falling block is block number $m$. Please compute how many placements after it lands satisfy that there is no cell which is empty but has a filled cell directly above it. In other words, compute how many placements satisfy that in every column, only a continuous segment of cells at the bottom is filled. Two placements are considered different if and only if there exists a cell that is filled in one placement but not filled in the other.

The first line contains two integers, representing the number of columns $n$ and the index $m$ of the next falling block. The second line contains $n$ integers. The $i$-th integer $a_i$ means that in the $i$-th column, only the bottom continuous $a_i$ cells are filled.

Output one integer in one line, representing the answer.

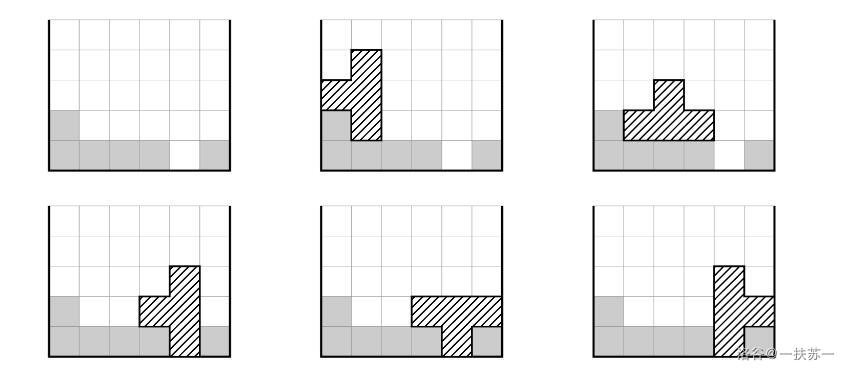
#### Explanation for Sample 1 Among the six figures below, the upper-left figure is the initial grid, and the other five figures are the five valid cases.  #### Constraints For all test points, it is guaranteed that: - $1 \leq n \leq 100$, $1 \leq m \leq 7$. - $0 \leq a_i \leq 100$. #### Note **This problem is translated from [COCI2006-2007](https://hsin.hr/coci/archive/2006_2007/) [Regional Competition](https://hsin.hr/coci/archive/2006_2007/regional_tasks.pdf) *T2 TETRIS***. Translation credit: @[一扶苏一](https://www.luogu.com.cn/user/65363)。 Translated by ChatGPT 5