P6483 [COCI 2010/2011 #4] PARKET

There is an $n$ by $m$ grid. The cells on the outer border are red, and all other cells are black. Given the number of red cells $r$ and the number of black cells $b$, find a feasible pair of values $n$ and $m$.

The input consists of one line with two integers, representing the number of red cells $r$ and the number of black cells $b$.

Output one line with two integers, representing the number of rows $n$ and the number of columns $m$ of the grid. If there are multiple solutions, output the one with the largest $n$.

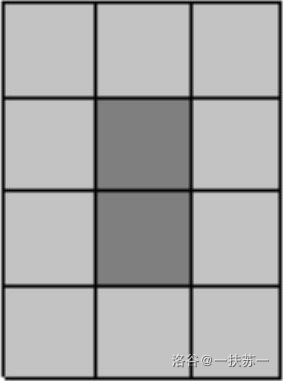
#### Explanation of Sample 2 The output grid is shown in the figure: light-colored cells represent red, and dark-colored cells represent black.  #### Constraints For all testdata, it is guaranteed that $8 \leq r \leq 2 \times 10^6$ and $1 \leq b \leq 2 \times 10^{6}$. It is guaranteed that at least one solution exists. #### Note **This problem is translated from [COCI2010-2011](https://hsin.hr/coci/archive/2010_2011/) [CONTEST #4](https://hsin.hr/coci/archive/2010_2011/contest4_tasks.pdf) *T2 PARKET***. Translation by @[一扶苏一](https://www.luogu.com.cn/user/65363). Translated by ChatGPT 5